Dec 22

The “parent” functions

By Tutor GuyNo Comments

 

Do you know your parent functions? I’m surprised every year when some of my students don’t know how to graph some of the elementary functions they’ve learned in class. Your chances for success in precalc and calculus are significantly better if you memorize the shapes of these ten functions. No excuses, no shortcuts. Just learn them.

 y = xn (Power functions)

 

 

 

 

 

 

 

 

 

 

y = |x| (absolute value function)

 

 

 

 

 

 

 

 

 

 

y = ⌊x⌋ (Greatest integer function)

 

 

 

 

 

 

 

 

 

 

y = √x

 

 

 

 

 

 

 

 

 

 

y = 1/x

 

 

 

 

 

 

 

 

 

y= bx (exponential function – growth and decay)

 

 

 

 

 

 

 

 

 

y = log x

 

 

 

 

 

 

 

 

y = sin x and y = cos x

 

 

 

 

 

 

 

 

y = tan x

 

Algebra 2, Calculus, Precalc/Trig
, , , , , , ,
Dec 15

Calculating probabilities as a fraction

By Tutor GuyNo Comments

 

The first day you are asked to find probabilities, the questions are relatively simple:

  • What is the probability of rolling a 2 or a 3 on a standard die? [Ans: 2/6 = 1/3]
  • What is the probability of drawing a five from a standard deck of cards? [Ans: 4/52 = 1/13]

But very quickly, the problems get a lot more complicated:

  • What is the probability of flipping a coin ten times and getting exactly 8 heads?
  • What is the probability of being dealt a full house (three of a kind plus a pair) in a five card poker hand?
  • A class has 14 boys and 12 girls. If the teacher randomly creates a new seating chart, what is the probability that the six students in the front row comprise exactly four boys and two girls?

How do you attack these problems? The best way is to think of probability as a fraction. The numerator counts all the ways the specified event can occur, and the denominator counts all the ways any event can occur:

Your event
Any event

Then you use combinatorics to count all the possibilities on the top and on the bottom. Let’s see how we can use this method to answer the three questions posed above:

 

 

 

(Note that this question could also be treated as a binomial probability and solved that way.)

Algebra 2, Statistics
, , , ,
Dec 08

Factoring sums and differences of fifth powers (and higher!) when the power is odd

By Tutor GuyNo Comments

 

Occasionally, you are required to factor a polynomial that is in the form of a sum or difference of two power terms (i.e., xn – yn). In my last post, I showed you a simple procedure you can learn to help you factor the binomial if the value of the power is 4 or greater and the power is even. [If you are reading this post, you should already be familiar with factoring the difference of two squares and the difference of two cubes. Check this website for posts on those procedures.] In this post, I show you a procedure (more complicated than the others, I admit) that you can use to factor these binomials when the power is odd.

First, let’s see how this works on some examples:

 

 

 

 

Do you see the pattern? When factoring an – bn or an + bn (for n odd), there is always a linear term a ± b, where the plus or minus sign is the same as in the original binomial. The remaining factor is a little more complicated, but it does have a simple pattern. Each term consists of the first term in the binomial (with its exponent decreasing from n – 1 to 0) and the second term in the binomial with its exponent increasing from 0 to n – 1. In the first example above, the x term decreased from x4 to x0. The 2 term increased from 20 to 24. If you started with the difference of two powers, all of the signs in the second factor are plus signs. If you started with the sum of the two powers, the first sign in the second factor is a minus sign and the signs alternate after that.

Algebra 2, Precalc/Trig
, , , , , ,
Dec 01

Factoring differences of fourth powers (and higher!) when the power is even

By Tutor GuyNo Comments

 

Occasionally, you are required to factor a polynomial that is in the form of a difference of two power terms (i.e., xn – yn). There is a simple procedure you can learn to help you factor the polynomial if the value of the power is 4 or greater and the power is even. [If you are reading this post, you should already be familiar with factoring the difference of two squares and the difference of two cubes. Check this website for posts on those procedures.]

First, let’s see how this works on some examples:

 

 

 

 

 

 

You can see that whenever the power is even, you treat the binomial as the difference of two squares and find its factors. If the factors are still the sum and difference of perfect squares, you repeat the process with the term that is the difference of two squares. If the factors are now the sum and difference of perfect cubes, you follow the method for factoring the sum or difference of two cubes. If the powers are sums and differences of odd powers higher than 3, there is another procedure to factor them. You can find another post on this website that shows that procedure.

Algebra 2, Precalc/Trig
, , , , , ,
Nov 24

Using ratios to solve physics problems when variables change values

By Tutor GuyNo Comments

 

A common question when you learn an equation in physics is “how is the value of one variable affected when a second variable is changed?” For example, “An astronaut has a weight of 200 N as she stands on the surface of a certain moon of Jupiter. How much would she weigh standing on a second moon that has three times the mass and twice the radius of the first moon?”

Many students find this a difficult problem to calculate, but it is actually something that you can solve quickly with just a bit of thought. The trick is to recognize that problems of this sort can be solved with a simple ratio. Let’s see how to solve the problem posed above. We will call the astronaut’s weight on the first moon F1 and on the second moon F2. The masses of the two moons are M1 and M2 respectively and their radii are r1 and r2. The mass of the astronaut is MA. Then from the universal law of gravitation:

F_1= \dfrac{GM_1M_A}{r_1^{\; 2}}

 and

F_2= \dfrac{GM_2M_A}{r_2^{\; 2}}

But we are told that the mass of the second moon is three times the mass of the first moon and its radius is twice the radius of the first moon. That means that M2 = 3 M1 and r2 = 2 r1. We substitute these expressions into the equation for F2 above. This gives

F_2= \dfrac{G(3M_1)M_A}{({2r_1)}^2}= \dfrac{3GM_1M_A}{4r_1^{\; 2}}

 Now divide this equation by the first equation and all the variables cancel out:

\dfrac{F_2}{F_1}=\dfrac{\dfrac{3GM_1M_A}{4r_1^{\; 2}}}{\dfrac{GM_1M_A}{r_1^{\; 2}}}=\dfrac{3}{4}

\therefore F_2= \dfrac{3}{4}F_1=150 \; N

With some practice, you will find that you can do many of these problems in your head!

Physics
Nov 17

SI unit prefixes

By Tutor GuyNo Comments

Even with scientific notation, very large numbers and very small numbers can be awkward to work with. That is why scientists have developed a set of standard prefixes that are attached to a unit to indicate multiples of that unit. Each of the prefixes represents a particular power of ten. There are currently 24 prefixes in use:

 

Prefixes greater than 1

Factor

Name

symbol

1030

quetta

Q

1027

ronna

R

1024

yotta

Y

1021

zetta

Z

1018

exa

E

1015

peta

P

1012

tera

T

109

giga

G

106

mega

M

103

kilo

k

102

hecto

h

101

deka

da

 

Prefixes less than 1

Factor

Name

symbol

10-1

deci

d

10-2

centi

c

10-3

milli

m

10-6

micro

μ

10-9

nano

n

10-12

pico

p

10-15

femto

f

10-18

atto

a

10-21

zepto

z

10-24

yocto

y

10-27

ronto

r

10-30

quecto

q

 

Do you have to memorize all of these? No. If you are a high school chemistry or physics student, you should know the prefixes in blue above. If you are an AP chemistry or AP physics student, you should also learn the prefixes in red. If you plan to be a scientist or an engineer, it wouldn’t hurt you to learn the rest, but the extreme prefixes are not so common.

Why do the prefixes skip three powers of 10? This allows us to use numbers that are always between 1 and 999. This is easiest to explain with an example. Let’s say we are measuring very small electrical currents. The following table shows how we would state the values without scientific notation, with scientific notation, and with prefixes. You can see how convenient this prefix method is:

Current Scientific notation Prefix notation
0.50 A 5.0 x 10-1 A 500 mA
0.050 A 5.0 x 10-2 A 50 mA
0.0050 A 5.0 x 10-3 A 5 mA
0.00050 A 5.0 x 10-4 A 500 μA
0.000050 A 5.0 x 10-5 A 50 μA
0.0000050 A 5.0 x 10-6 A 5 μA
0.00000050 A 5.0 x 10-7 A 500 nA
0.000000050 A 5.0 x 10-8 A 50 nA
0.0000000050 A 5.0 x 10-9 A 5 nA
0.00000000050 A 5.0 x 10-10 A 500 pA
Chemistry, Physics
, , ,
Nov 10

Divisibility rules

By Tutor GuyNo Comments

 

You always need to simplify fractions and radicals before you box your final answer. In order to simplify these, you need to be able to factor integers. There was a teacher at my middle school who urged his students to “learn your gozintas!” In other words, know whether a number goes into the number you are factoring. Now that calculators are so common, many students today don’t think they need to learn their gozintas. However, the divisibility rules for the first six prime numbers are so easy to learn, you will benefit from knowing them.

   A number is divisible by ___ if:    Examples

2

 Last digit is 0, 2, 4, 6, 8 478 ends in 8, so it is divisible by 2.

8349 doesn’t end in 0, 2, 4, 6 or 8 so it is not divisible by 2.

3

 Sum of digits is divisible by 3 8349 is divisible by 3 because 8+3+4+9 = 24 which is divisible by 3. [See note below.]

1450 is not divisible by 3 because 1+4+5+0 = 10 which is not divisible by 3.

5

 Last digit is 0, 5 1450 is divisible by 5.

3157 is not divisible by 5.

7

 Twice the last digit subtracted from the remaining digits is divisible by 7

(Take the last digit and double it. Subtract this from the original number after the last digit is removed.)

 3157 is divisible by 7 because 315 – 2*7 = 315-14 = 301 which is divisible by 7. [See note below.]

4563 is not divisible by 7 because 456 – 2*3 = 456 – 6 = 450 which is not divisible by 7.

9

 Sum of digits is divisible by 9 4563 is divisible by 9 because 4+5+6+3 = 18 which is divisible by 9. [See note below.]

90827 is not divisible by 9 because 9+0+8+2+7 = 26 which is not divisible by 9.

11

 Sum of odd digits – sum of even digits is divisible by 11

(Here, odd and even digits refer to their place in the number, not their value. For example, if you have a 9 digit number, add the 1st, 3rd, 5th, 7th and 9th digits and subtract the sum of the 2nd, 4th, 6th and 8th digits. If this number is divisible by 11, the original number is divisible by 11.)

 90827 is divisible by 11 because (9+8+7) – (0+2) = 24 – 2 = 22 which is divisible by 11. [See note below.]

478 is not divisible by 11 because (4+8)-7 = 5 which is not divisible by 11.

 

Note: What if you do the test for divisibility by 3, 7, 9 or 11, but you don’t know whether the number you obtained is divisible by the number you are testing? Then just do the test again. Let’s test a large number to see how this works.

Example 1: Is 999,999 divisible by 3 or by 9?

9+9+9+9+9+9 = 54. And 5+4 = 9. So 999,999 is divisible by 3 and by 9.

Example 2: Is 999,999 divisible by 7?

99,999 – 18 = 99,981. And 9998 – 2 = 9986. And 998 – 12 = 986. And 98 – 12 = 84. And 8 – 8 = 0, which is divisible by 7. So 99,999 is divisible by 7! (And so are 99,981 and 9986 and 986 and 84!)

No matter how large your original number, you can just keep repeating the test until you know your answer for certain.

Algebra 1, Algebra 2, Geometry
, , ,
Nov 03

Surface area and volume formulas for solids

By Tutor GuyNo Comments

 

Solid figures can be scary for a lot of students. There are a lot of confusing formulas and it can be difficult to draw a three-dimensional figure on a flat sheet of paper. But solids can be tamed if you categorize them by the number of bases. Note in the table below that the formulas for prisms and cylinders are exactly the same, as are the formulas for pyramids and cones. You will have the most success if you memorize these formulas—then you just plug in the given values to find the unknown values. If you are struggling with the formulas, print this page out and paste it into your binder until you are more comfortable with them.

Bases

 Figure Lateral surface area Volume

2

 Prism ph Bh
Cylinder ph = 2 \pi rh Bh= \pi r^2h

1

 Pyramid 1/2 p \ell 1/3 Bh
Cone 1/2 p \ell = \pi r \ell 1/3 Bh = 1/3 \pi r^2h

0

 Sphere 4 \pi r^2 4/3 \pi r^3

p = perimeter; h = height; ℓ = slant height; B = Base area; r = radius

An added wrinkle that can make pyramids difficult is that you are not always given all the necessary information to plug into the formulas. What do you do? Remember what you’ve learned about regular polygons and use the Pythagorean Theorem! Let’s look at an example. The pyramid in the figure is a regular pyramid with a hexagonal base. The edge length is 6 cm and the radius of the base is 3 cm. Find the lateral surface area and the volume of the pyramid.

 

 

 

 

 

 

 

 

 

You can see from the pyramid formulas above that we need to know the perimeter of the base and the slant height to find the area, and we need to know the Base area and the height to find the volume. And we don’t have any of these numbers! It seems like we don’t have enough information. But there was one other clue that will help us solve this puzzle. The pyramid is regular, which means the foot of the altitude touches the center of the base, and the base is regular. If you draw the altitude, it forms a right triangle with the radius and the edge.

 

 

 

 

 

 

 

 

 

Using the Pythagorean Theorem (or recognizing this as a 30°-60°-90° triangle), you can easily find the altitude is

h=3 \sqrt{3}

Because the base is a regular hexagon, you can also find the edge length, perimeter and the apothem:

s=3\rightarrow p=18; a= \dfrac{3 \sqrt{3}}{2}

 Finally, the triangle formed by the altitude, apothem and slant height is also a right triangle.

 

 

 

 

 

 

 

 

 

From the Pythagorean Theorem again, we find the slant height:

{\ell}^2={\left( \dfrac{3 \sqrt{3}}{2} \right)}^2 +{\left( 3 \sqrt{3} \right)}^2= \dfrac{135}{4} \rightarrow \ell = \dfrac{3 \sqrt{15}}{2}

 Now we have all the information we need to find the area and volume. Just plug it all in:

LA = \dfrac{1}{2} p \ell = \dfrac{1}{2}(18)\!\!\left( \dfrac{3 \sqrt{15}}{2} \right) = \dfrac{27 \sqrt{15}}{2}

V = \dfrac{1}{3}Bh=\dfrac{1}{3} \! \left( \dfrac{1}{2}ap \right)\! h= \dfrac{1}{3} \cdot \dfrac{1}{2} \!\left( \dfrac{3 \sqrt{3}}{2} \right) \! (18)(3 \sqrt{3})= \dfrac{81}{2}

 Whew! Yes, that’s a lot of work, but just break the problem down piece by piece and you can solve these problems like a pro!

Geometry
, , , ,
Oct 27

Simplifying “3-stack” and “4-stack” fractions

By Tutor GuyNo Comments

 

I had a physics student a number of years ago who worked a complicated problem and ended up with the following (I’ve changed the actual numbers to make our work here easier to follow):

\dfrac{(2)(3)}{4}=\dfrac{(5)(6)(7)B}{(8)(9)}

Of course, his next step was to solve for B. It should be clear to you, as it was to him, that he needed to multiply both sides by 8 and 9 and divide by 5, 6 and 7. That is what he did. But this is how he wrote the solution:

B= \dfrac{9 \cdot \left( \dfrac{ \left(\dfrac{ 8 \cdot \left( \dfrac{(2)(3)}{4} \right)}{5} \right)}{6} \right)}{7}

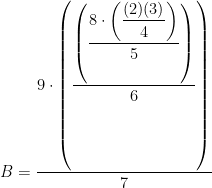
His expression was totally correct, and he found the correct value of B, but he made the problem so much harder than he needed to. He created a fraction with five different stacks in it and he needed all those parentheses to keep track of which number was a numerator and which was a denominator.

This is an extreme case of what I see so many students do: they create “3-stack” and “4-stack” fractions all the time when they are simplifying problems. Let’s look at two examples. I’ll solve them with “bad” solutions and then with much smarter solutions (I don’t simplify the answers here because I want to focus on the first step of the solution):

Example 1. Solve:

3x= \dfrac{2}{5}

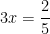
Bad solution:

x= \dfrac{\dfrac{2}{5}}{3}

 

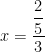
Smarter solution:

x= \dfrac{2}{5 \cdot 3}

Example 2. Solve:

\dfrac{4}{7}x=\dfrac{2}{5}

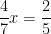
 Bad solution:

x= \dfrac{\dfrac{2}{5}}{\dfrac{4}{7}}

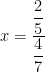
 Smarter solution:

x= \dfrac{2 \cdot 7}{5 \cdot 4}

You can see that the smarter solutions are simpler to read and easier to simplify.

It is easy to train yourself to write answers as “2-stack” fractions if you remember one simple rule:

Respect the vinculum.

Um, respect the what?!?

The vinculum. When you write a fraction, the horizontal line that separates the numerator from the denominator is called the vinculum. No one ever talks about it, but it’s a very powerful symbol. It tells you to multiply by every number that is above it and divide by every number that is below it. And it’s as easy as that. So when you are simplifying expressions like the ones in the two examples above or the more complicated example at the beginning of this post, all you need to do is to put numbers that are multiplied above the vinculum and numbers that are divided below the vinculum. And what happens if you are multiplying or diving by a fraction? Then put the numerator on top and the denominator on the bottom if you are multiplying. Flip the fraction over first if you’re dividing (as I did in Example 2). When you do this, you will end up with a 2-stack fraction that can be easily evaluated. Let’s look at the original problem again:

\dfrac{(2)(3)}{4}=\dfrac{(5)(6)(7)B}{(8)(9)}

To solve for B, you will multiply by 8 and 9, so they go on top. And you will divide by 5, 6 and 7, so they go on the bottom. In one step, you’ve solved for B as follows:

B= \dfrac{2 \cdot 3 \cdot 8 \cdot 9}{5 \cdot 6 \cdot 7}

Compare that to the monstrosity at the beginning. So much easier!

P.S. You don’t really have to remember the name “vinculum”. Most people don’t know what the line is called and don’t care. Chances are good your math teacher doesn’t even know the term. To make things even more bizarre, when you write a fraction with a slash instead of a horizontal line like this—2/3 – the slash is called a “virgule”.  Most people don’t know that one and don’t care about it either. All you have to remember is that the horizontal line in a fraction tells you to multiply on top and divide on the bottom.

Algebra 1, Algebra 2, Calculus, Physics, Precalc/Trig
, , ,
Oct 20

Angles in circles and arc measures

By Tutor GuyNo Comments

 

When angles are formed by chords, secants and tangents in a circle, there are several formulas that help you determine the arc measures and angle measures that are formed. With a little bit of thought, you can often find values for all of the arcs and angles around the circle. For many students, the equations are difficult to remember. Your best approach is to categorize the angle by the location of the vertex. Then learn the rule for the angles with that particular vertex. There are four possibilities:

  • Central angles: This is an angle whose vertex is at the center of the circle. For all central angles, the angle measure is equal to the arc measure of the subtended arc.
  • Inscribed angles: These angles have their vertex on the circle. They can be chord-chord angles or chord-tangent angles. For these angles, the angle measure is one half the arc measure of the subtended arc.
  • Internal angles: These are angles whose vertex is in the interior of the circle but not at the center. For these angles, the angle measure is one half the sum of the arc measures of the two subtended arcs.
  • External angles: These are angles whose vertex is outside the circle. They can be secant-secant angles or secant-tangent angles. For these angles, the angle measure is one half the difference of the arc measures of the subtended arcs.

Geometry
, , ,
< OlderNewer >
Blue Taste Theme created by Jabox