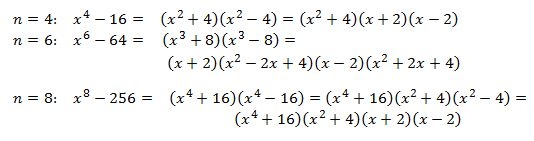Occasionally, you are required to factor a polynomial that is in the form of a difference of two power terms (i.e., xn – yn). There is a simple procedure you can learn to help you factor the polynomial if the value of the power is 4 or greater and the power is even. [If you are reading this post, you should already be familiar with factoring the difference of two squares and the difference of two cubes. Check this website for posts on those procedures.]
First, let’s see how this works on some examples:
You can see that whenever the power is even, you treat the binomial as the difference of two squares and find its factors. If the factors are still the sum and difference of perfect squares, you repeat the process with the term that is the difference of two squares. If the factors are now the sum and difference of perfect cubes, you follow the method for factoring the sum or difference of two cubes. If the powers are sums and differences of odd powers higher than 3, there is another procedure to factor them. You can find another post on this website that shows that procedure.