Archive

Dec 29

Sum( and Seq( commands on your calculator

By Tutor GuyNo Comments

 

Can you find the sum of the following series?

\displaystyle \sum_{i=1}^{15}\dfrac{2n+1}{3n-2}

 This is neither an arithmetic nor a geometric series, so you don’t have a formula for it. This would be a tedious problem to do by hand. Fortunately, your graphing calculator can do these problems quickly and efficiently.

There are two functions you need to use on your calculator. The seq( command creates a sequence of terms based on a rule that you give. The sum( command adds together the terms in a sequence. Both functions are found on the LIST menu on your calculator. The seq( command is on the OPS submenu and the sum( command is on the MATH submenu.

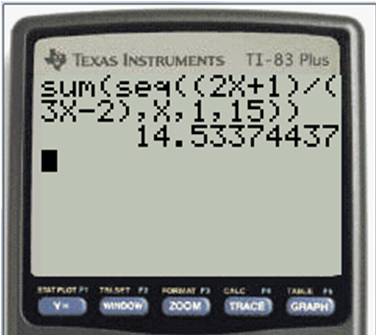
To sum a series, you combine the two commands. If you have the new operating system on your calculator, it will prompt you for the entries when you select the seq( command. If you have the old operating system, you need to know the syntax for the command. The syntax for the series above is:

 sum(seq((2x + 1)/(3x – 2),x,1,15))

Note that the seq( command has four parameters in the parentheses. From left to right, these are 1) the rule for the nth term of the sequence; 2) the variable name; 3) the first value of the variable; and 4) the final value of the variable. Now all you need to do is type this in to your calculator and let it do the crunching:

 

Dec 22

The “parent” functions

By Tutor GuyNo Comments

 

Do you know your parent functions? I’m surprised every year when some of my students don’t know how to graph some of the elementary functions they’ve learned in class. Your chances for success in precalc and calculus are significantly better if you memorize the shapes of these ten functions. No excuses, no shortcuts. Just learn them.

 y = xn (Power functions)

 

 

 

 

 

 

 

 

 

 

y = |x| (absolute value function)

 

 

 

 

 

 

 

 

 

 

y = ⌊x⌋ (Greatest integer function)

 

 

 

 

 

 

 

 

 

 

y = √x

 

 

 

 

 

 

 

 

 

 

y = 1/x

 

 

 

 

 

 

 

 

 

y= bx (exponential function – growth and decay)

 

 

 

 

 

 

 

 

 

y = log x

 

 

 

 

 

 

 

 

y = sin x and y = cos x

 

 

 

 

 

 

 

 

y = tan x

 

Dec 08

Factoring sums and differences of fifth powers (and higher!) when the power is odd

By Tutor GuyNo Comments

 

Occasionally, you are required to factor a polynomial that is in the form of a sum or difference of two power terms (i.e., xn – yn). In my last post, I showed you a simple procedure you can learn to help you factor the binomial if the value of the power is 4 or greater and the power is even. [If you are reading this post, you should already be familiar with factoring the difference of two squares and the difference of two cubes. Check this website for posts on those procedures.] In this post, I show you a procedure (more complicated than the others, I admit) that you can use to factor these binomials when the power is odd.

First, let’s see how this works on some examples:

 

 

 

 

Do you see the pattern? When factoring an – bn or an + bn (for n odd), there is always a linear term a ± b, where the plus or minus sign is the same as in the original binomial. The remaining factor is a little more complicated, but it does have a simple pattern. Each term consists of the first term in the binomial (with its exponent decreasing from n – 1 to 0) and the second term in the binomial with its exponent increasing from 0 to n – 1. In the first example above, the x term decreased from x4 to x0. The 2 term increased from 20 to 24. If you started with the difference of two powers, all of the signs in the second factor are plus signs. If you started with the sum of the two powers, the first sign in the second factor is a minus sign and the signs alternate after that.

Dec 01

Factoring differences of fourth powers (and higher!) when the power is even

By Tutor GuyNo Comments

 

Occasionally, you are required to factor a polynomial that is in the form of a difference of two power terms (i.e., xn – yn). There is a simple procedure you can learn to help you factor the polynomial if the value of the power is 4 or greater and the power is even. [If you are reading this post, you should already be familiar with factoring the difference of two squares and the difference of two cubes. Check this website for posts on those procedures.]

First, let’s see how this works on some examples:

 

 

 

 

 

 

You can see that whenever the power is even, you treat the binomial as the difference of two squares and find its factors. If the factors are still the sum and difference of perfect squares, you repeat the process with the term that is the difference of two squares. If the factors are now the sum and difference of perfect cubes, you follow the method for factoring the sum or difference of two cubes. If the powers are sums and differences of odd powers higher than 3, there is another procedure to factor them. You can find another post on this website that shows that procedure.

Blue Taste Theme created by Jabox