Bay Area Tutoring

Jan 08

Finding the roots of a quadratic in vertex form

By Tutor GuyNo Comments

If you have taken algebra 2, you know you can write quadratic functions in three forms:

Standard form: $y = ax^2 + bx +c$
Vertex form: $y = a(x-h)^2 + k$
Factored form: $y = a(x-r_1)(x-r_2)$

No matter which of the forms you have, you are often asked to find the roots (x-intercepts). The factored form is already done for you: the roots are the values of $r_1$ and $r_2$ . If your equation is in standard form, you use the quadratic formula. But what do you do if you have a quadratic in vertex form? Most students are taught to expand the equation into standard form (and then use the quadratic formula). But there’s a quick shortcut that is pretty easy to use. In fact, you can write the roots by inspection. If $0 = a(x-h)^2 + k$ , then the roots are

$x = h \pm \sqrt{\dfrac{-k}{a}}$

There are three cases:

$k=0$ : There is one (double) root;
$a \text{ and } k$ have different signs: the two roots are real;
$a \text{ and } k$ have the same sign: the two roots are complex.

In the complex case, you can express the roots as

$x = h \pm \sqrt{\dfrac{k}{a}} \; i$

Here are two quick examples:

Example 1: $0 = 2(x-3)^2 + 6$

Using the formula above, the roots can be written immediately as

$x = 3 \pm \sqrt{\dfrac{6}{2}} \; i =3 \pm \sqrt{3} \; i$

Example 2: $0 = 2(x-3)^2 - 8$

The roots are:

$x = 3 \pm \sqrt{\dfrac{8}{2}} = 3 \pm 2 = 1 \text{ and } 5$

Algebra 2, Precalc/Trig

quadratic, roots

Jan 01

Making excellent histograms on your calculator

By Tutor GuyNo Comments

Your graphing calculator will make superb histograms from data you enter. If you have tried to do this, but your histograms don’t look the way you expect, follow this procedure. You have to tweak the x-min, x-max, and x-scale values to match your preferences. Let’s say that you have collected the following data (perhaps they are the heights of 30 people in your class):

61.0    61.5     62.0    65.0    65.5     65.5     66.0     66.0
66.5    66.5     67.0    67.0    67.5     68.0     68.5     68.5
69.0    69.0    69.0    69.5    69.5     70.0     70.5     72.0
72.0    72.0    74.0    74.0    75.0     75.5

1. Determine the smallest class value and the class width. For this data set, I would display the data in five classes. We can set the smallest class value to 61, the largest class value to 76 and therefore the class width will be 3.

2. On your calculator, enter the data into a list. Here I’ve put it into L1.

3. Go to STAT PLOT and turn one of the plots on.

4. Select the histogram type and if necessary specify the Xlist location.

5. Press zoom and select 9 (ZoomStat). Your graph probably won’t look right, but we’ll fix that.

6. Press the WINDOW button and set Xmin= to the smallest class value, Xmax= to the largest class value, and Xscl= to the class width. You might also need to adjust the Ymin and Ymax values.

7. Press GRAPH, and admire your excellent histogram.

Algebra 2, Calculator, Statistics

graphing, histograms

Dec 25

graphing sec x, csc x functions

By Tutor GuyNo Comments

Graphing secant functions and cosecant functions can be daunting for students. But you can tame them if you recognize how they are related to graphs of sine and cosine functions. If you can graph the associated sine or cosine function, then secant and cosecant graphs will be pretty easy for you.

We will demonstrate this process with an example: Draw the graph of

$-3 \csc{(2x+\dfrac{\pi}{2})} - 1$

The first step for you is to graph a different function. If you are asked to graph a cosecant curve as in this example, change csc to sin and graph that instead. If you are graphing a secant function, change sec to cos and graph that instead. In our example, we will graph

$-3 \sin{(2x+\dfrac{\pi}{2})} - 1$

I showed you how to graph sine and cosine functions in a previous post, so check that out if you need help. In that post, we graphed the sine function listed above. Here, we will assume you have already graphed the sine function:

Next, put in the vertical asymptotes everywhere the sine curve crosses the midline:

Then use the asymptotes to place the branches of the cosecant function. Also, notice that the minimum points of the cosecant curve touch the maximum points of the sine curve and vice versa:

That’s all there is to it! You can erase the sine curve (in green) or you can leave it. I usually draw in the sine or cosine curve in light pencil or as a dashed line, so that it is obvious which curve is the secant or cosecant curve. Here, the red curve is the graph we desire.

Precalc/Trig

cosecant, graphing, secant, trig

Dec 18

Determining rate order from concentration vs. time data

By Tutor GuyNo Comments

As a reaction proceeds, we can measure the concentration of a reactant at various times. Then we use this data to determine the reaction order. For example, here’s the data for some arbitrary reaction during its first 30 seconds:

Time (s)	[A] (M)
0	0.100
5	0.0632
10	0.0400
15	0.0253
20	0.0160
25	0.0101
30	0.0064

To find the reaction order, we create three graphs. One is [A] vs. time, a second is ln [A] vs. time and the third is 1/[A] vs. time. If the first graph is linear, the reaction is zeroth order with respect to [A]. If the ln of concentration graph is linear, the reaction is first order, and if the reciprocal concentration graph is linear, the reaction is second order. In the old days (before calculators), we would calculate all the numbers and graph the data by hand and hope that one was obviously linear. Here, I used my graphing calculator to quickly generate three scatter graphs, shown below:

It should be pretty obvious that the red graph (ln [A] vs time) is the only linear graph, and that means the reaction is first order with respect to [A]. The rate equation is thus: rate = k[A] and the absolute value of the slope of the line (found using a linear regression) is the rate constant k.

What if the data has a bit of variability in it and the data doesn’t fit perfectly on a straight line on any of the three graphs? With your graphing calculator, create the three scatter graphs as I did above, then perform a linear regression on each graph. The graph with r² closest to 1.0 will be the correct graph.

Chemistry

chemical kinetics, reaction rates

Dec 11

Determining rate order from initial reaction rate

By Tutor GuyNo Comments

When you are studying chemical kinetics, a typical problem will look something like this:

Compounds A and B react together according to the following reaction:

A + 2 B → C + D

The following initial reaction rate data was collected. Determine the rate equation for this reaction.

Rxn	[A]	[B]	Initial rxn rate
1	0.0500 M	0.0500 M	1.2 x 10^-4 M/s
2	0.100 M	0.0500 M	2.4 x 10^-4 M/s
3	0.100 M	0.100 M	9.6 x 10^-4 M/s

These problems are pretty easy to solve if you have learned exponential equations in algebra 2. The trick is to compare two different reactions where only one compound changes its concentration. For example, if you compare reaction 1 with reaction 2, you will see that [A] changes and [B] is the same. If you compare reactions 2 and 3, you see that [B] changes and [A] is held constant. However, when you compare reactions 1 and 3, both [A] and [B] change. So do not compare reactions 1 and 3.

Next, remember that your answer will be in the form

Rate = k [A]^m [B]ⁿ

Therefore, your job is to determine the values of m, n, and k. You do this by taking the values from the table and plugging them into this equation.

Let’s find the value of m first. You need two equations where [A] changes and [B] does not—that is, equations 1 and 2.

$\begin{matrix} (2) \quad & 2.4 \cdot 10^{-4} = k(0.100)^m(0.0500)^n \\ (1) \quad & 1.2 \cdot 10^{-4} = k(0.0500)^m(0.0500)^n \end{matrix}$

Now divide the first equation by the second. The magic here is that k and the term with the n exponent both cancel out, leaving you with a simple expression:

$2.0 = 2^m$

It should be pretty obvious that m = 1. What if the numbers don’t divide evenly and you end up with an equation such as

$2.03 = 1.982^m?$

Unless told otherwise, you can assume that the exponent is supposed to be an integer, and therefore m= 1 in this problem too.

Now, let’s solve for n. We need two equations where [B] changes and [A] does not. That would be equations 2 and 3. Set it up the same way as before:

$\begin{matrix} (3) \quad & 9.6 \cdot 10^{-4} = k(0.100)^m(0.100)^n \\ (2) \quad & 2.4 \cdot 10^{-4} = k(0.100)^m(0.0500)^n \end{matrix}$

And divide as before:

$4.0 = 2^n$

Thus n = 2. Now we can solve for k by taking any of the three original equations and plugging in all the given values. Let’s use equation 3.

$9.6 \cdot 10^{-4} = k(0.100)^1(0.100)^2$

Solving this equation gives k = 0.96. Therefore, our final answer is

Rate = 0.96 [A] [B]²

Now here’s an additional trick I give you at no extra charge: If you are pretty good with exponents and scientific notation, you should see that you can often solve for the values of m and n in your head. In our first step, the rate doubled when [A] doubled, so the rate with respect to A is first order (m = 1). In our second step, the rate quadrupled when [B] doubled, so the rate with respect to B is second order (n = 2). (That was certainly a lot easier than the work we did above!) Then plug the known values into the rate equation to solve for k.

Chemistry

chemical kinetics, reaction rates

Dec 04

Differential rate law vs. integrated rate law

By Tutor GuyNo Comments

When we study rates of chemical reactions, we look for an equation that describes the reaction rate. The equation can be in one of two forms, known as the differential rate law and the integrated rate law.

If you have taken calculus, you’ll recognize these names and you even know how to derive the integrated law from the differential law. If you haven’t taken calculus, don’t worry! You probably won’t be asked to derive the equations. However, you should recognize each form of the law for zeroth, first and second order reactions.

The differential rate law gives the reaction rate as a function of the concentration of the reactants. The integrated rate law gives the concentration as a function of time. Both equations are useful, and you will probably use both in your chemistry class.

The table below shows the two rate laws for each reaction order in terms of a single reactant A.

Order	Differential rate law	Integrated rate law
Zeroth	Rate = k	$[A] = -kt + [A]_0$
First	Rate = k[A]	$\ln{[A]} = -kt + \ln{[A]_0}$
Second	Rate = k[A]²	$\dfrac{1}{[A]} = kt + \dfrac{1}{[A]_0}$

You might have noticed that each of the integrated law equations is in the form y = mx + b, the equation for a line. In the old days (before graphing calculators), this is the method that chemists used to determine the reaction order. If the graph of concentration vs. time is a straight line, the reaction is zeroth order. If the graph of ln(concentration) vs. time is a straight line, the reaction is first order. And if the graph of 1/concentration vs. time is a straight line, the reaction is second order.

Chemistry

chemical kinetics, reaction rates

Nov 27

Solving integrals of the form tan^m x secⁿ x

By Tutor GuyNo Comments

In a recent post, I showed you how to approach integrals of the form

$\displaystyle \int \sin^m{x} \; \cos^n{x} \; dx$

In this post, we look at the similar integral of the form

$\displaystyle \int \tan^m{x} \; \sec^n{x} \; dx$

As before, m and n are integers. The technique we use requires m to be odd or n to be even and we factor out terms of the associated function. We demonstrate with an example. Evaluate:

$\displaystyle \int \tan^5{x} \; \sec^6{x} \; dx$

Here, m is odd and n is even, so we can factor either the tan x or the sec x function. We’ll do it both ways here to show both techniques. First, when m is odd, we factor out a single power of both tan x and sec x and the rest of the integral follows the method we saw in the sin^m x cosⁿx integral example:

$\displaystyle \int \tan^5{x} \; \sec^6{x} \; dx = \int \sec{x} \; \tan{x} \; \tan^4{x} \; \sec^5{x} \; dx =$

$\displaystyle \int \sec{x} \; \tan{x} \; (\tan^2{x})^2 \; \sec^5{x} \; dx = \int \sec{x} \; \tan{x} \; (\sec^2{x} - 1)^2 \; \sec^5{x} \; dx =$

$\displaystyle \int \sec{x} \; \tan{x} \; (\sec^4{x} - 2 \sec^2{x} + 1) \; \sec^5{x} \; dx =$

$\displaystyle \int \sec{x} \; \tan{x} \; (\sec^9{x} -2 \sec^7{x} + \sec^5{x}) \; dx =$

Then letting u = sec x leads to

$\displaystyle f(x) = \frac{1}{10} \sec^{10}{x} - \frac{1}{4} \sec^8{x} + \frac{1}{6} \sec^6{x} + C$

Now let’s do the same integral the other way. When n is even, we factor out a sec² x, and the rest of the process is similar to the first method:

$\displaystyle \int \tan^5{x} \; \sec^6{x} \; dx = \int \sec^2{x} \; \tan^5{x} \; \sec^4{x} \; dx =$

$\displaystyle \int \sec^2{x} \; \tan^5{x} \; (\sec^2{x})^2 \; dx = \int \sec^2{x} \; \tan^5{x}\; (\tan^2{x} + 1)^2 \; dx =$

$\displaystyle \int \sec^2{x} \; \tan^5{x} \; (\tan^4{x} +2\tan^2{x} + 1) \; dx =$

$\displaystyle \int \sec^2{x} (\tan^9{x} + 2 \tan^7{x} + \tan^5{x}) \; dx$

Then letting u=tan x,

$\displaystyle f(x) = \frac{1}{10} \tan^{10}{x} + \frac{1}{4} \tan^8{x} + \frac{1}{6} \tan^6{x} + C$

Wait! That’s not the same integral we got in the method above. Well, actually, it is! After a trig substitution (1 + tan² x = sec² x) and a lot of messy algebra, you can show they are the same function. I’ll leave you to work out the details. Better yet, graph them both on your graphing calculator and you will see they are the same.

Calculus

integration

Nov 20

Solving integrals of the form sin^m x cosⁿ x when m and n are even

By Tutor GuyNo Comments

In my last post, I showed you the method for integrating functions of the form

$\int \sin^m{x} \; \cos^n{x} \; dx$

when either m or n is odd. If they are both even, the process is more complicated. In this post, I’ll show you how to attack this problem. There are two different methods you can use; if one doesn’t work so well, try the other. We will demonstrate both methods here with an example. Let’s integrate

$\int \sin^2{x} \; \cos^4{x} \; dx$

Method 1

First, rewrite the integral so that the factors are powers of sin²x and cos²x.

$\int \sin^2{x} \; (\cos^2{x})^2 \; dx$

Use the power reducing formulas

$\sin^2{x} = \frac{1}{2}(1- \cos{2x}) \text{ and } \cos^2{x} = \frac{1}{2}(1+\cos{2x})$

to replace both the sin²x and the cos²x terms.

$\displaystyle \int \sin^2{x} \; (\cos^2{x})^2 \; dx = \int \left(\frac{1}{2}(1- \cos{2x})\right) \left(\frac{1}{2} (1+\cos{2x}) \right)^2 \; dx$

Then expand each term and multiply it all out (hey, I said it was more complicated…)

$\displaystyle \int \left(\frac{1}{2}(1- \cos{2x})\right) \left(\frac{1}{2} (1+\cos{2x}) \right)^2 \; dx =$

$\displaystyle \frac{1}{8} \int (1- \cos{2x})(1 + 2 \cos{2x} + \cos^2{2x}) \; dx =$

$\displaystyle \frac{1}{8} \int 1 + 2 \cos{2x} + \cos^2{2x} - \cos{2x} - 2 \cos^2{2x} - \cos^3{2x} \; dx$

$\displaystyle \frac{1}{8} \int 1 + \cos{2x} - \cos^2{2x} - \cos^3{2x} \; dx$

Now we are finally ready to integrate. The first two terms can be integrated by inspection. The third term is attacked by using the power reducing formula. In the last term, the exponent is odd, so apply the technique we used in the last blog post:

$\displaystyle \frac{1}{8} \int 1 + \cos{2x} - \frac{1}{2} (1+\cos{4x}) - \cos{2x}\cos^2{2x} \; dx =$

$\displaystyle \frac{1}{8} \int 1 + \cos{2x} - \frac{1}{2} (1+\cos{4x}) - \cos{2x}(1- \sin^2{2x}) \; dx =$

$\displaystyle \frac{1}{8} \int \frac{1}{2} - \frac{1}{2} \cos{4x} + \cos{2x} \sin^2{2x} \; dx =$

$\displaystyle \frac{1}{8} \left( \frac{1}{2}x - \frac{1}{8} \sin{4x} + \frac{1}{6} \sin^3{2x} \right) + C = \frac{1}{16}x - \frac{1}{64} \sin{4x} + \frac{1}{48} \sin^3{2x} + C$

Whew!

Method 2:

First, rearrange terms so that there is a power of (sin x cos x).

$\displaystyle \int \sin^2{x} \cos^4{x} \; dx = \int \sin^2{x} \cos^2{x} \cos^2{x} \; dx =$

$\displaystyle \int (\sin{x} \cos{x})^2 \cos^2{x} \; dx$

Then use the double angle formula $\sin{x} \cos{x} = \frac{1}{2} \sin{2x}$ and the power reducing formulas as necessary:

$\displaystyle \int (\sin{x} \cos{x})^2 \cos^2{x} \; dx = \int \left(\frac{1}{2} \sin{2x} \right)^2 \left(\frac{1}{2} (1+ \cos{2x}) \right) \; dx$

Expand the terms and multiply out:

$\displaystyle \int \left(\frac{1}{2} \sin{2x} \right)^2 \left(\frac{1}{2} (1+ \cos{2x}) \right) \; dx = \frac{1}{8} \int \sin^2{2x} (1+ \cos{2x}) \; dx =$

$\displaystyle \frac{1}{8} \int \sin^2{2x} + \sin^2{2x} \cos{2x} \; dx = \frac{1}{8} \int \frac{1}{2} (1- \cos{4x}) + \sin^2{2x} \cos{2x} \; dx =$

$\displaystyle \frac{1}{8} \left( \frac{1}{2}x - \frac{1}{8} \sin{4x} + \frac{1}{6} \sin^3{2x} \right) + C = \frac{1}{16}x - \frac{1}{64} \sin{4x} + \frac{1}{48} \sin^3{2x} + C$

Note that this is the same result as in Method 1 above.

Calculus

integration

Nov 13

Solving integrals of the form sin^m (x) cosⁿ (x)

By Tutor GuyNo Comments

An important class of integrals is of the form:

$\int \sin^m{x} \; \cos^n{x} \; dx$

where m and n are integers. If either m or n is odd, factor out a single power of that function and rewrite the integral to solve with a u substitution. This is best demonstrated with an example:

$\int \sin^5{x} \; \cos^7{x} \; dx$

Here, both m and n are odd, so we can select either function to factor. The process is easier when you pick the smaller of the two exponents, so let’s choose the sin x and we factor out one power as follows:

$\int \sin{x} \; \sin^4{x} \; \cos^7{x} \; dx$

We then rewrite the even power as a power of sin² x so that we can apply a trig identity:

$\int \sin{x} \; \sin^4{x} \; \cos^7{x} \; dx = \int \sin{x} \; (\sin^2{x})^2 \; \cos^7{x} \; dx =$

$\int \sin{x} \; (1-\cos^2{x})^2 \; \cos^7{x} \; dx = \int \sin{x} \; (1-2 \cos^2{x} + \cos^4{x}) \; \cos^7{x} \; dx =$

$\int \sin{x} \; (\cos^7{x} -2 \cos^9{x} + \cos^{11}{x}) \; dx$

This is easily integrated with a u substitution (let u = cos x):

$\dfrac{1}{8} \cos^8{x} - \dfrac{1}{5} \cos^{10}{x} + \dfrac{1}{12} \cos^{12}{x} + C$

So what do you do if both m and n are even? Well, most students just skip the problem and go on to the next one. ☺ But if you want to see the technique, look for my next blog post.

Calculus

integration

Nov 06

Making sense of math induction

By Tutor GuyNo Comments

Do you know the sum of the first five positive odd numbers? How about the sum of the first 20 positive odd numbers? The first 100? Wouldn’t it be great if there were a formula for the sum of the first n positive odd numbers so we could easily answer this question? Let’s see if we can find a pattern:

n	Expression	Sum
1	1	1
2	1 +3	4
3	1 + 3 + 5	9
4	1 + 3 + 5 + 7	16
5	1 + 3 + 5 + 7 + 9	25

It certainly appears that the sum of the first n positive odd numbers is n². Or, if we write this symbolically:

$\displaystyle \sum_{i=1}^n (2i - 1) = n^2$

We’ve just shown that this formula is true for the first five values of n, but how do we know it is true for every value of n? We could test our theorem for n = 6, n = 7, n = 8, and so forth. But you can see that this process would take us a very long time to show it for every value of n. Like, forever! Fortunately, there is a better method for proving conjectures of this sort. It is called mathematical induction. Math induction is a very powerful tool in analysis. If you think about it, it allows us to prove an infinite number of theorems. And we can do this in only three steps!

How does math induction work? It depends on a subtle idea: if the theorem is true for one particular value of n (say n= k) and we can use this fact to show that it’s true for the next value of n (that is, n=k+1), then it will be true for every value of n ≥ k. That is, one proof turns into an infinite number of proofs! How is this possible? Because each value of n leads to the next value of n. If it’s true for n=3 then we’ve shown it’s true for n=4. But since it’s true for n=4, we’ve also shown it’s true for n=5. And therefore it’s also true for n=6, and then n=7, etc. Most textbooks that cover math induction use a dominoes analogy—if you knock down the first domino, it knocks down the second, the second knocks down the third and so on.

Here are the three steps in math induction, and you will see that they are quite simple to describe:

Step 1: prove the theorem is true for n=1. This is a really easy step. You just plug in n=1 into the theorem and show that it is true. (Note: on occasion, you will start at a value of n greater than 1. This does not change the validity of the process.)

Step 2: Assume that the theorem is true for n = k. (Note that you aren’t even proving anything in this step. You just write out what the theorem would look like if it were true for n=k.)

Step 3: Use the expression in Step 2 to show that the theorem is true for n=k+1. (You usually do this by applying a little bit of algebra.)

That’s all there is to it! Let’s see how it works on the theorem we proposed above. We restate the theorem here for convenience:

$\displaystyle \sum_{i=1}^n (2i - 1) = n^2$

Step 1: Prove for n = 1.

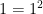$1 = 1^2$ (See? This is a really easy step.)

Step 2: Assume for n=k

$1+3+5+ \dots + (2k-1) = k^2$ (Just write down the formula for n = k.)

Step 3: Prove for n = k+1

$1+3+5+ \dots + (2k-1) = k^2 \; \; \text{[line 1]}$

$1+3+5+ \dots + (2k-1)+(2k+1) = k^2 + (2k+1) \; \; \text{[line 2]}$

$k^2 + (2k+1) = (k+1)^2 \; \; \text{[line 3]}$

[This step is a little harder to follow, so I’ve numbered the lines to explain the process.

Line 1 is simply a repeat of Step 2. I wrote it here for clarity; you don’t need to repeat your work.
In line 2, I’ve added (2k + 1) to both sides. That’s a valid algebra operation, so if Line 1 is true, Line 2 is also true. Why did I add (2k +1)? Because it’s the next term in the sum on the left side of the equation.
In Line 3, I’ve simplified the right side of the equation.]

But (k+1)² is exactly what our theorem says the right side of the equation will be when n = k+1. So the assumption that the theorem is true for n=k led to the conclusion that it is also true for n=k+1. And our proof is complete.

Precalc/Trig

math induction

Tutor Guy Homework Tips