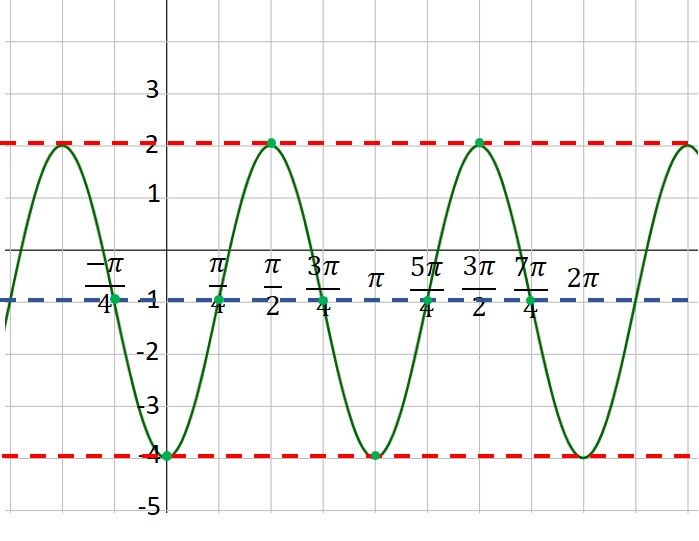
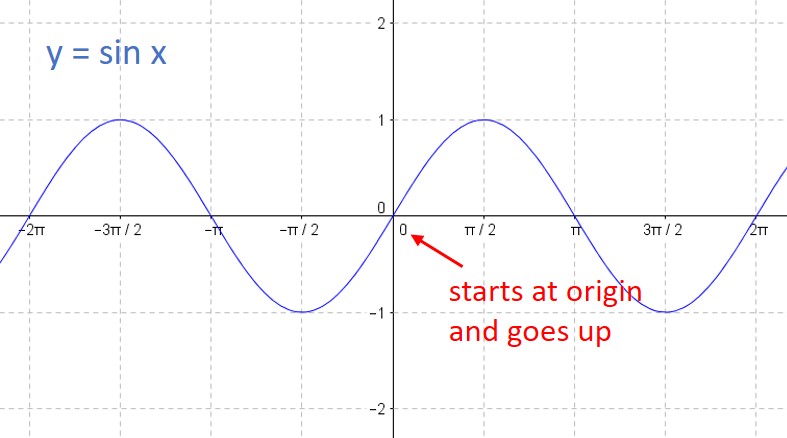
One of the most complicated skills you need to learn in your trig class is how to graph sine and cosine functions. This scares a lot of students, but you can tame this process if you make one simple observation: Every sine and cosine curve has exactly the same shape! No matter the amplitude or period or phase shift, the curve looks just like this:

You only need to place the graph in its proper position on the coordinate axes. This is (mostly) easy to accomplish if you can remember only two things about the sine and cosine parent curves:
1) The sine curve y = sin x “starts” at the origin and goes up to its maximum, while the cosine curve y = cos x “starts” at its maximum.
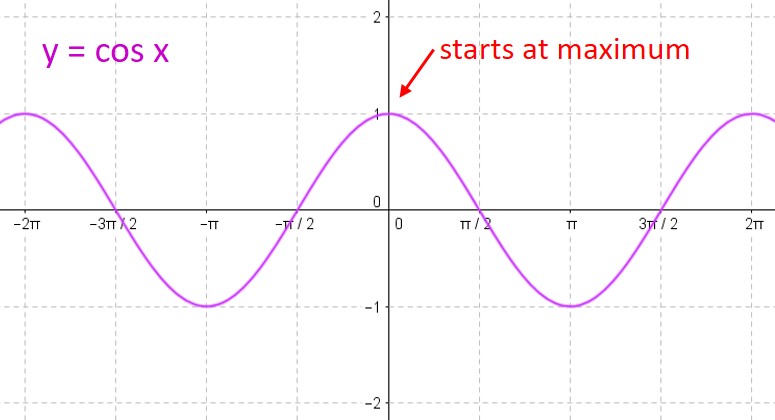
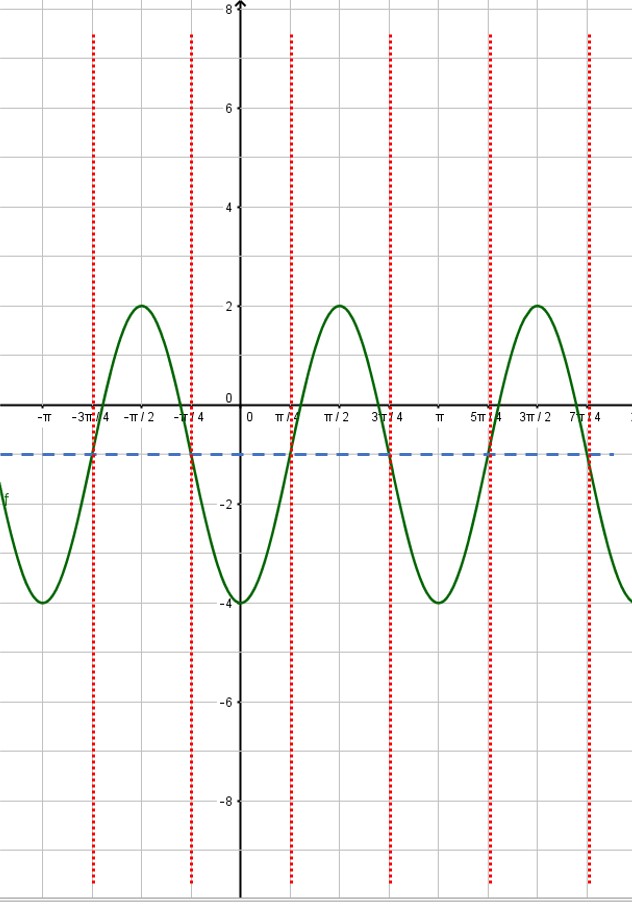
2) For either curve, you can break one period into four equal intervals. At each interval, the curve moves from its midline to the maximum to the midline to the minimum to the midline to the maximum to… over and over again. So all you need to do is find the starting point, and plot the points on the curve at each ¼-period interval.
We will always write our functions in standard form:
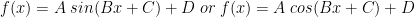
(Note that some textbooks prefer to write the formula in a slightly different form:
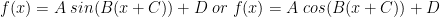
We will discuss how that affects your work below.)
Each of the constants A, B, C & D affects the position of the curve and you need to analyze this before you graph the curve. Let’s look at each of them in turn:
A: The absolute value of this number tells you the amplitude of your curve.
B: The period of your curve is determined by dividing 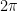 by B.
by B.
C: The phase shift is found by dividing -C by B. A positive value means the phase shift is to the right. A negative value means the phase shift is to the left. (If your class uses the version of the equation above with the B factored out, then the phase shift is equal to C.)
D: The vertical shift is equal to D.
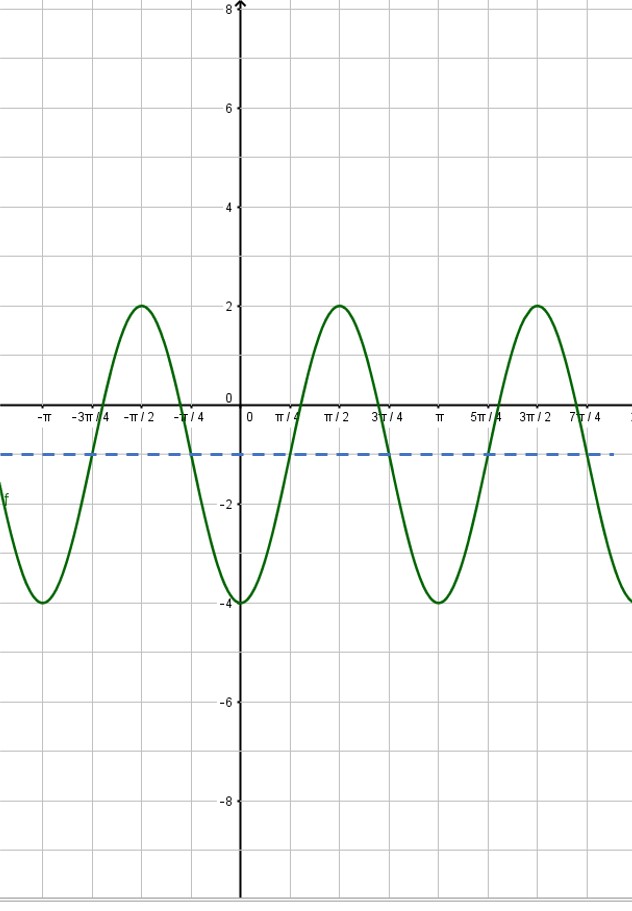
Here’s an example to show how you would calculate all these values.
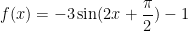
Here, A = -3; B = 2; C =  ; and D = -1. Therefore,
; and D = -1. Therefore,
Amplitude = |-3| = 3
Period = 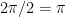
Phase shift =  (that is,
(that is, 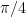 units to the left)
units to the left)
Vertical shift = -1
When you need to graph a sine or cosine curve, always determine these four values first. Then you are ready to graph the function. We’ll do that in our next post.