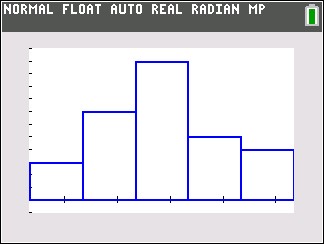
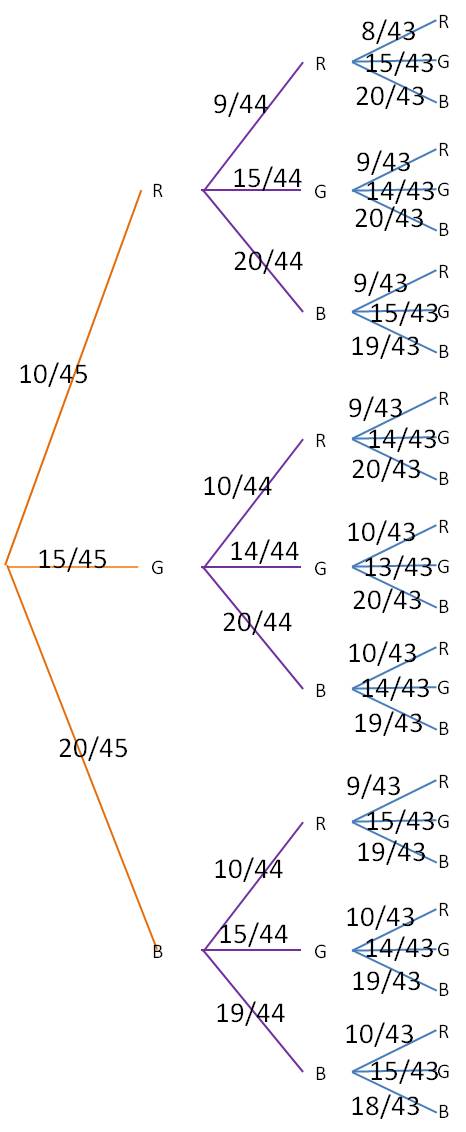
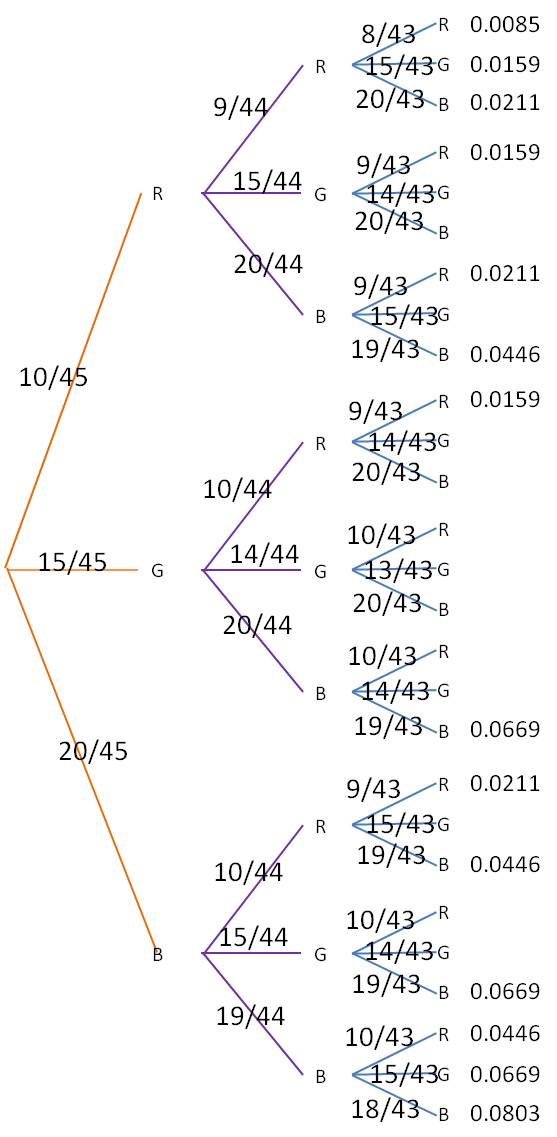
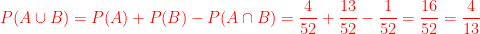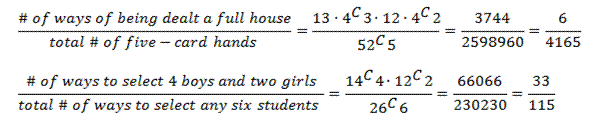Two of the many formulas you learn in statistics are referred to as the Multiplication Rule and the Addition Rule. How do you figure out when to use each one? This is actually a pretty easy one. The multiplication rule is used to determine the probability of two events both happening, one after the other. The key word to look for in a problem is ‘and’.
Example 1: You draw a single card from a standard deck, replace it and draw a second card. What is the probability you draw a seven first AND a heart second? Because you want the probability of both events occurring, you use the multiplication rule.
The addition rule is used to find the probability that either one of two events occurs. The key word here is “or’.
Example 2: You draw a single card from a standard deck, replace it and draw a second card. What is the probability you draw a seven on the first draw OR a heart on the second draw? Because you want the probability of either event occurring, you use the addition rule.
How do the rules work? The multiplication rule comes in two forms. If the two events are independent, that is, if the probability of the second event does not change when the first event occurs, then the formula is simple:
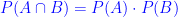
If the probability of the second event depends on the first event occurring, the formula is modified slightly to show this:

You can see from either formula why this is called the multiplication rule. The addition rule is just slightly more complicated.

You can see from this formula why it is called the addition rule. Let’s solve both problems.
Example 1: The two events are independent, so we use the first version of the rule:

Example 2: (Note that we use the result from Example 1 in solving this problem.)