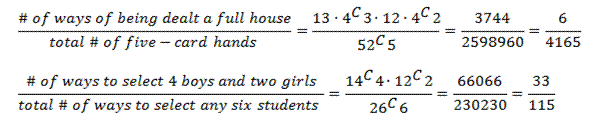The first day you are asked to find probabilities, the questions are relatively simple:
- What is the probability of rolling a 2 or a 3 on a standard die? [Ans: 2/6 = 1/3]
- What is the probability of drawing a five from a standard deck of cards? [Ans: 4/52 = 1/13]
But very quickly, the problems get a lot more complicated:
- What is the probability of flipping a coin ten times and getting exactly 8 heads?
- What is the probability of being dealt a full house (three of a kind plus a pair) in a five card poker hand?
- A class has 14 boys and 12 girls. If the teacher randomly creates a new seating chart, what is the probability that the six students in the front row comprise exactly four boys and two girls?
How do you attack these problems? The best way is to think of probability as a fraction. The numerator counts all the ways the specified event can occur, and the denominator counts all the ways any event can occur:
Your event
Any event
Then you use combinatorics to count all the possibilities on the top and on the bottom. Let’s see how we can use this method to answer the three questions posed above:
(Note that this question could also be treated as a binomial probability and solved that way.)