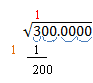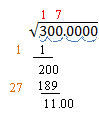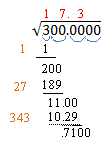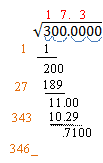Archive

For the Algebra 2 category

Jan 08

Finding the roots of a quadratic in vertex form

By Tutor GuyNo Comments

 

If you have taken algebra 2, you know you can write quadratic functions in three forms:

  • Standard form: y = ax^2 + bx +c
  • Vertex form: y = a(x-h)^2 + k
  • Factored form: y = a(x-r_1)(x-r_2)

No matter which of the forms you have, you are often asked to find the roots (x-intercepts). The factored form is already done for you: the roots are the values of r_1 and r_2 . If your equation is in standard form, you use the quadratic formula. But what do you do if you have a quadratic in vertex form? Most students are taught to expand the equation into standard form (and then use the quadratic formula). But there’s a quick shortcut that is pretty easy to use. In fact, you can write the roots by inspection. If 0 = a(x-h)^2 + k , then the roots are

x = h \pm \sqrt{\dfrac{-k}{a}}

There are three cases:

  • k=0 : There is one (double) root;
  • a \text{ and } k have different signs: the two roots are real;
  • a \text{ and } k have the same sign: the two roots are complex.

In the complex case, you can express the roots as

x = h \pm \sqrt{\dfrac{k}{a}} \; i

Here are two quick examples:

Example 1: 0 = 2(x-3)^2 + 6

Using the formula above, the roots can be written immediately as

x = 3 \pm \sqrt{\dfrac{6}{2}} \; i =3 \pm \sqrt{3} \; i

Example 2: 0 = 2(x-3)^2 - 8

The roots are:

x = 3 \pm \sqrt{\dfrac{8}{2}} = 3 \pm 2 = 1 \text{ and } 5

Jan 01

Making excellent histograms on your calculator

By Tutor GuyNo Comments

 

Your graphing calculator will make superb histograms from data you enter. If you have tried to do this, but your histograms don’t look the way you expect, follow this procedure. You have to tweak the x-min, x-max, and x-scale values to match your preferences. Let’s say that you have collected the following data (perhaps they are the heights of 30 people in your class):

61.0    61.5     62.0    65.0    65.5     65.5     66.0     66.0
66.5    66.5     67.0    67.0    67.5     68.0     68.5     68.5
69.0    69.0    69.0    69.5    69.5     70.0     70.5     72.0
72.0    72.0    74.0    74.0    75.0     75.5

1. Determine the smallest class value and the class width. For this data set, I would display the data in five classes. We can set the smallest class value to 61, the largest class value to 76 and therefore the class width will be 3.
 2. On your calculator, enter the data into a list. Here I’ve put it into L1.
 3. Go to STAT PLOT and turn one of the plots on.

 4. Select the histogram type and if necessary specify the Xlist location.
 5. Press zoom and select 9 (ZoomStat). Your graph probably won’t look right, but we’ll fix that.
 6. Press the WINDOW button and set Xmin= to the smallest class value, Xmax= to the largest class value, and Xscl= to the class width. You might also need to adjust the Ymin and Ymax values.
 7. Press GRAPH, and admire your excellent histogram.
Oct 30

Managing exponential equations

By Tutor GuyNo Comments

 

Many algebra 2 students get intimidated by exponential equations because the answers are rarely nice simple integers. But keep in mind that like all the equations you solved in algebra 1, you are merely trying to find the value of x that satisfies the equation. The process is a little more complicated because your variable is now in an exponent, but just follow these steps and you’ll soon be an exponential expert!

There are two types of exponential equations and they each have a preferred strategy for solving them. The first type has an exponential expression on both sides of the equal sign, and the two bases are both powers of the same number. The second type of equation has exponential expression with bases that aren’t powers of the same number (or has an exponential expression on only one side of the equals sign).

Type 1. Bases that are powers of the same number. Check out these two problems.

\text{a.  } 4^{x+4} = 8^{x-1}

Solution: note that the two bases (4 and 8) are both powers of 2. We rewrite both bases as powers of 2 and simplify:

\text{a.  } 4^{x+4} = 8^{x-1} \rightarrow (2^2)^{x+4} = (2^3)^{x-1} \rightarrow (2)^{2x+8} = (2)^{3x-3}

Now we take advantage of a simple property that says if a^x = a^y \text{ then } x = y.  Since both bases are the same, we just set the exponents equal to each other:

(2)^{2x+8} = (2)^{3x-3} \rightarrow 2x + 8 = 3x - 3. Solving this gives x = 11.

 

\text{b.  } 5^{4x} = 125^{x+1}

Solution: note that both bases are powers of 5. Proceed exactly as in the last problem:

\text{b.  } 5^{4x} = 125^{x+1} \rightarrow 5^{4x} = (5^3)^{x+1} \rightarrow 5^{4x} = 5^{3x+3} \rightarrow 4x = 3x + 3 \rightarrow x = 3

 

Type 2: Bases are not powers of the same number. To solve these types of problems, you will need to use logarithms. Here are two examples.

\text{a.  } 2^{x+3} = 12

Solution: The bases (2 and 12) are not powers of the same base. (Always check this first, because the method shown in the Type 1 examples above is almost always simpler.) So we solve by taking logs of each side. In the old days (before graphing calculators) you would need to use a common log (base 10) or a natural log (base e). I’ll show you that method first:

\text{a.  } 2^{x+3} = 12 \rightarrow \ln{(2^{x+3})} = \ln{12} \rightarrow (x+3) \ln{2} = \ln{12}

\therefore x = \dfrac{\ln{12}}{\ln{2}} - 3 \approx 0.5840

If your graphing calculator has the logbase command on it, you can solve this problem even more easily by taking a log base 2 of each side:

\text{a.  } 2^{x+3} = 12 \rightarrow \log_2{(2^{x+3})} = \log_2{12} \rightarrow x+3 = \log_2{12}

\therefore x = \log_2{12} - 3 \approx 0.5840

 

\text{b.  } 5^{x+3} = 7^{x-2}

Solution: This looks a lot uglier than the previous example, but the solution starts the same way. Take the log of both sides:

\text{b.  } 5^{x+3} = 7^{x-2} \rightarrow \log_5{(5^{x+3})} = \log_5{(7^{x-2})} \rightarrow (x+3) = (x-2) \log_5{7}

We need to collect the x terms to solve for x, so distribute on the right side and solve:

(x+3) = (x-2) \log_5{7} \rightarrow (x+3) = x \; \log_5{(7)} - 2 \; \log_5{(7)} \rightarrow

3 + 2 \log_5{(7)} = x \; \log_5{(7)} - x \rightarrow 3 + 2 \; \log_5{7} = x (\log_5{(7)} - 1) \rightarrow

x = \dfrac{3 + 2 \; \log_5{(7)}}{\log_5{(7)} - 1} \approx 25.92

Whew!

Sep 11

Calculating permutations and combinations

By Tutor GuyNo Comments

 

When counting up the number of ways an event can occur, you use the formulas for permutations and combinations. You should be familiar with the nPr and nCr commands on your calculator, and this is the easiest way to evaluate these problems. But if your calculator doesn’t have these functions, there is a fairly simple way to set up these operations. This is the way we had to calculate permutations and combinations when calculators did not have these functions built in. Practice a couple of these examples and you’ll see that you can calculate permutations and combinations almost as quickly as your calculator can do it.

Calculating nPr

To calculate nPr, you will multiply together r consecutive numbers, starting with n and counting down. For example, 12P 3 is equal to 12*11*10 = 1320. We started with 12 (the value of n) and counted down to 10 so that we had 3 numbers (3 is the value of r). As another example, 7P5 = 7*6*5*4*3 = 2520.

Calculating nCr

To calculate nCr, create a fraction. The numerator is the same as above; that is, start with n and count down r consecutive numbers. The denominator is the smaller of r! and (n-r)!. For example,12P3 is

\dfrac{12*11*10}{1*2*3}

Before you calculate this fraction, simplify it. All of the terms in the denominator will always cancel out with terms in the numerator, leaving you with just numbers in the numerator to multiply together. For example,

\dfrac{12*11*10}{1*2*3} = 2 * 11 * 10 = 220

To calculate 7C5, note that 7C5 = 7C2 . Then,

\dfrac{7*6}{1*2} = 7 * 3= 21

Aug 21

An algorithm for calculating the square root of a number

By Tutor GuyNo Comments

 

How do you find the square root of a number? You use a calculator, of course! But what if you can’t find your calculator? Did you know there’s an algorithm that will allow you to derive a square root of a number? My dad taught it to me a long time ago before calculators were around. It would surprise me if anyone you know under the age of 40 has ever seen it. It’s a slow, painstaking process, so only use it if you have a lot of time to waste. Frankly, I’d recommend waiting until you get a new calculator, but in case you’re interested, here it is. It’s easiest to explain with an example. Let’s find the square root of 300. Because we want to calculate some digits after the decimal point, we will write it as 300.0000

\sqrt{300.0000}

The first step is to separate the digits into groups of two. Starting from the decimal point, mark off each pair of digits. If there are an odd number of digits to the left of the decimal point, the leftmost digit will be a single digit and not a pair. Then start from the decimal point again and count off the digits to the right by twos. In our example, the “3” in 300 is a single digit and all the others are pairs.

 

 

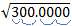
Now we are ready to calculate. Our first digit is a three. We find the largest integer whose square is less than this number. Since 12 = 1 < 3 and 22 = 4 >3, our number is 1. We place a 1 above the 3, just like we are doing a long division problem.

 

 

Next, copy this digit on the line below the 300.

 

 

This next step looks a lot like a long division problem. Multiply the (red) 1 by the (tan) 1 and put the product under the 3. Then subtract, and bring down the next two digits. Our example will look like this:

 

 

 

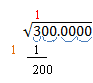
Now it gets a little strange. Take the (red) number above the 300 and double it. Write this number on the next line down on the left and add an underscore. 1 doubled is 2, so our example now looks like this:

 

 

 

The underscore is a place holder for an unknown digit. We need to find a single digit that we will place above the line (over the “00”) and in the placeholder. We want the product of these two numbers to be as large as possible without being larger than the current remainder. Let’s say we decide the digit is 6. Then 6 ·26 = 156. If the digit is 7, then 7 ·27 = 189. If the digit is 8, then 8 ·28 = 224. This is larger than 200, so our digit is 7. We place it above the radical and in the placeholder as shown below. Do the multiplication and subtraction as before. Write the remainder and bring down the next two digits. Our example now looks like this:

 

 

 

 

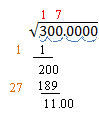
Now we repeat this process over and over for each new digit. Double the number above the radical and add a placeholder. 17 ·2 = 34, so our problem now looks like this:

 

 

 

 

Again, we need a digit above the line and in the placeholder so that the product is less than the remainder. 3·343 = 1029 < 1100.   4·344 = 1376 >1100. So the digit we want is 3. Do the multiplication and subtraction and bring down the next two digits. Our example looks like this:

 

 

 

 

 

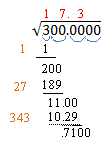
Let’s do it one more time. Double the number over the radical and add a placeholder:

 

 

 

 

 

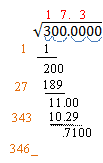
The next digit we need is a 2. (2·3462 = 6924 < 7100; while 3·3463 = 10389 > 7100). Multiply and subtract and bring down the next two digits.

 

 

 

 

 

 

17.32 is a pretty good approximation of the square root of 300. You can repeat this process as often as you want to get even more digits in your solution. The next number we would write on the left would be 3464_. You can see that the number on the left gets bigger with each step, so the process gets pretty unwieldy. If you need more than three or four digits in your square root, make sure you have a lot of paper, or go find that calculator!

Aug 14

Graphing sine and cosine functions like a pro

By Tutor GuyNo Comments

 

When graphing a sine or cosine curve, the first thing you must do is determine the amplitude, period, phase shift and vertical shift. See my previous post (Graphing Sine and Cosine Functions – Intro) if you need help with this analysis. In this post, we will graph the function

\displaystyle f(x) = -3 \sin (2x + \frac{\pi}{2}) -1

We quickly determine the four values we need:

Amplitude = |-3| = 3

Period = 2 \pi /2 = \pi

Phase shift = -(\pi /2)/2 = - \pi/4  (that is, \pi /4 units to the left)

Vertical shift = -1

 

This is all the information we need in order to complete the graph. Just follow this procedure step-by-step.

 1. Put values on the coordinate axes. On the y-axis, you typically make each square equal to one unit, but you can change this if you want. To determine the scale on the x-axis, take the period and divide by 4. This will be the scale on the x-axis. In our example, the period is \pi , so each square will be \pi /4 . The vertical axis will be one unit per square. What do you do if your teacher gives you a grid with the numbers already in place? You should get a blank piece of graph paper and do your own grid!
 2. Use the vertical shift to draw a dashed line across the figure. This is the location of the midline of your graph. In our example, the vertical shift is -1, so we draw a dashed line at y= -1.
 3. Use the amplitude to draw two more dashed lines—one above the midline and one below. These represent the maximum and minimum values of your function. In our example, the amplitude is 3. Three units above -1 is 2—that’s our maximum dashed line. Three units below -1 is -4—that’s where our minimum is located.
 4. Plot the starting point of your graph, using the vertical shift and phase shift as a guide. Our function is a sine curve, which starts at the midline. The phase shift is \pi /4  to the left, so our initial point is \pi /4  units left of the y-axis. If our function had been a cosine curve, our initial point would be plotted on the maximum line instead of the midline (or on the minimum line if A is negative). It’s hard to see, but note that I’ve placed a green dot at the “start” point; the coordinates are ( - \pi /4, -1).
 5. Moving one square to the right at a time (because each square is one quarter of a period), plot points at the maximum, midline, minimum and midline. This is one period of your function. If you want to graph more than one period, continue the process. In our example, we’ve plotted points for two complete periods. Note that because A is a negative number (-3), our first point after the starting point is at the minimum instead of the maximum. Look closely, and you will see that I’ve placed a green dot every square to the right of our first point.
 6. Connect the dots with a nice smooth curve. You’ve graphed the sine curve like a pro!
Aug 07

Graphing sine and cosine functions– an Intro

By Tutor GuyNo Comments

 

One of the most complicated skills you need to learn in your trig class is how to graph sine and cosine functions. This scares a lot of students, but you can tame this process if you make one simple observation: Every sine and cosine curve has exactly the same shape! No matter the amplitude or period or phase shift, the curve looks just like this:

 

 

 

 

 

You only need to place the graph in its proper position on the coordinate axes. This is (mostly) easy to accomplish if you can remember only two things about the sine and cosine parent curves:

1)     The sine curve y = sin x “starts” at the origin and goes up to its maximum, while the cosine curve y = cos x “starts” at its maximum.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2)     For either curve, you can break one period into four equal intervals. At each interval, the curve moves from its midline to the maximum to the midline to the minimum to the midline to the maximum to… over and over again. So all you need to do is find the starting point, and plot the points on the curve at each ¼-period interval.

We will always write our functions in standard form:

f(x) = A \; sin(Bx+C) + D \; or \; f(x)= A \; cos(Bx+C) + D

(Note that some textbooks prefer to write the formula in a slightly different form:

f(x) = A \; sin(B(x+C)) + D \; or \; f(x)= A \; cos(B(x+C)) + D

We will discuss how that affects your work below.)

Each of the constants A, B, C & D affects the position of the curve and you need to analyze this before you graph the curve. Let’s look at each of them in turn:

A: The absolute value of this number tells you the amplitude of your curve.

B: The period of your curve is determined by dividing 2\pi by B.

C: The phase shift is found by dividing -C by B. A positive value means the phase shift is to the right. A negative value means the phase shift is to the left. (If your class uses the version of the equation above with the B factored out, then the phase shift is equal to C.)

D: The vertical shift is equal to D.

Here’s an example to show how you would calculate all these values.

\displaystyle f(x) = -3 \sin (2x + \frac{\pi}{2}) -1

Here, A = -3; B = 2; C = \pi/2 ; and D = -1. Therefore,

Amplitude = |-3| = 3

Period = 2 \pi /2 = \pi

Phase shift = - (\pi /2)/2 = - \pi /4  (that is, \pi /4 units to the left)

Vertical shift = -1

When you need to graph a sine or cosine curve, always determine these four values first. Then you are ready to graph the function. We’ll do that in our next post.

Aug 22

Using tree diagrams to find conditional probabilities

By Tutor GuyNo Comments

 

Those problems that ask you to find the probability of a series of events “without replacement” can be scary because the probabilities of each event keep changing. (These are known as conditional probability problems.) If the number of possible outcomes isn’t too large, you can tame these problems by using a tree diagram to simplify your calculations.

  1. For the first event, draw a tree branch for each possible outcome.
  2. At the end of each branch, draw a tree branch for each possible outcome of the second event.
  3. Continue until you have a column for every event.
  4. For every branch on the tree, write down the probability of that event occurring at that location.
  5. Then multiply all the branches from first event to last event to find the probability of any one outcome.
  6. Add various events together to get the probability of any compound outcome.

Here’s a simple example that shows how this process works. Let’s say you have a candy dish with 10 red candies, 15 green candies and 20 blue candies. You want to know the probability that you draw at least two red candies or at least two blue candies. There are a lot of different possibilities here, but a tree diagram simplifies everything greatly. Start by drawing a tree with every possible outcome (R, G and B in this example). Then from each outcome, draw another tree representing each outcome for the second draw. Repeat for the third draw. Your tree will look like this:
st-0501-tree

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(You can see that this process will get pretty unwieldy if there are too many outcomes or too many events.)

Next, label each branch with the probability for that outcome. Note that the probabilities change depending on which outcomes have already occurred. For our example, the tree would now look like this:
st-0502-tree

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Finally, for each of the branch ends at the right, multiply together all the probabilities leading to that endpoint. For example, the very top branch, which represents RRR, you would multiply 10/45*9/44*8/43 to find the probability of getting a red candy on all three draws. The final table looks like this (to make the table easier to read, we have calculated only those branches that represent at least two reds or at least two blues):
st-0503-tree

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

The probability of our desired event is then the sum of all of listed probabilities: 0.5352.

Mar 23

Using multiplicity of factors to characterize graphs of rational functions

By Tutor GuyNo Comments

 

Rational functions can be scary because there are so many details to manage. Check other posts on this website for information on how to graph rational functions. In this post, I look at one small clue that can help you figure out the behavior of a rational function as it approaches the vertical asymptotes. All you need to do is check the multiplicity of the factor in the denominator.

If the multiplicity of the factor is even, then the graph approaches +∞ from both sides of the asymptote, or it approaches -∞ from both sides of the asymptote.

If the multiplicity of the factor is odd, then the graph approaches +∞ on one side of the asymptote and approaches -∞ on the other side.

Here is an example that demonstrates this property:

\text{Graph } \dfrac {(x-2)(x+1)}{(x-1)(x+2)^2}

There are two vertical asymptotes for this function, at x=-2 and at x=1. The (x+2) factor is multiplicity 2 (even), so the graph approaches the same limit from both sides of the asymptote. The (x-1) factor is multiplicity 1 (odd), so the graph approaches opposite limits on either side of the asymptote. Here is the graph of the function, demonstrating this property:

Mar 16

Using multiplicity of factors to characterize graphs of polynomials

By Tutor GuyNo Comments

 

When you are asked to sketch the graph of a polynomial, you do not want to make a tree to calculate the values of various points. You don’t know where the “turning points” are, so you won’t be able to connect the dots for the points you plot. Instead, you need to fully factor the polynomial and use the zeroes you find to draw the polynomial. In addition, the multiplicity of each factor tells you whether the polynomial crosses the x-axis at that zero or “bounces”. The rule is very simple: If the factor has an odd multiplicity, the graph crosses the x-axis. If the multiplicity is even, the graph bounces.

multiplicity behavior at x ‑axis
odd crosses
even bounces

 

Example: Sketch the graph of

f(x)=x^3(x+1)(x-1)^2

Solution: First of all, plot the zeroes. For this problem, the zeroes are at x=-1, x=0, \text{ and } x=1.

 

 

 

 

 

 

 

Next, determine the degree of the polynomial. In this case, it is degree 6. (Add the exponents of all the factors: 3+1+2=6.) The degree tells you the end behavior, and you can draw arrows to show that the function will go to positive infinity on the left and the right.

 

 

 

 

 

 

 

 

Now you can sketch the graph. At x=-1, the zero is multiplicity 1, so the graph crosses the x-axis. At x=0, the zero is multiplicity 3, so the graph also crosses the x-axis. Note that for multiplicity 3, the graph doesn’t cross straight through the axis, but flattens out as it goes through. At x=1, the zero is multiplicity 2, so the graph bounces at the x-axis. The final sketch is shown below:

< Older
Blue Taste Theme created by Jabox