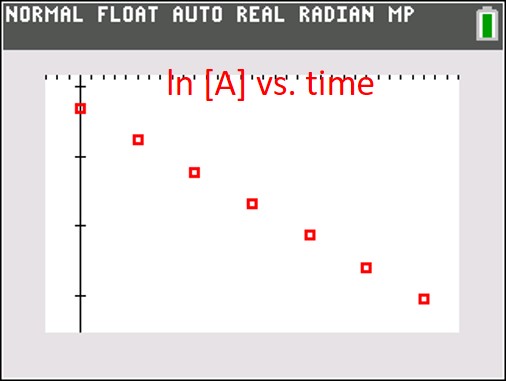
When balancing redox reactions, you must start by finding the number of electrons transferred in each half reaction. You usually can’t get the charges to balance if you don’t equate the electrons. In this post, I show you how to balance a redox reaction in an acidic solution.
Example 1: Balance the following reaction:
MnO4– + NO + H+ → Mn2+ + H2O + NO3–
Solution: To balance reactions like this, use the following four-step procedure:
- Determine the number of electrons transferred in each half reaction, and balance the electrons.
- Balance the oxygen atoms by adding water molecules.
- Balance the hydrogen atoms by adding H+ ions.
- Check you answer by verifying that the charges are balanced.
In this reaction, the Mn atom goes from an oxidation number of 7+ in the permanganate ion to an oxidation number of 2+. It has gained five electrons. The nitrogen atom goes from an oxidation number of 2+ in the nitric oxide to 5+ in the nitrate ion. It has lost three electrons. To balance the electrons, we need to make the total number of electrons transferred equal 15 (because that’s the least common multiple of three and five!). We multiply the Mn ions by 3 and the N compounds by 5:
3 MnO4– + 5 NO + H+ → 3 Mn2+ + H2O + 5 NO3–
The next step is to balance the oxygen atoms. There are 17 oxygen atoms on the left side of the reaction and 15 on the right side (before you include the water). Therefore we need two water molecules on the right:
3 MnO4– + 5 NO + H+ → 3 Mn2+ + 2 H2O + 5 NO3–
Finally, we balance the hydrogen atoms (there are four of them in the water molecule on the right) by adding 4 hydrogen ions on the left:
3 MnO4– + 5 NO + 4 H+ → 3 Mn2+ + 2 H2O + 5 NO3–
We check our work by verifying the charges balance. 3- (the permanganate ions) and 4+ (the hydrogen ions) gives a net charge on the left of 1+. 6+ (the manganese ions) and 5- (the nitrate ions) on the right also gives a net charge of 1+. We have succeeded!
Example 2: Complete and balance the following reaction. Assume it takes place in an acidic solution:
Cr2O72– + HSO3– → SO42– + Cr3+
Solution: In this reaction, the Cr atoms go from an oxidation number of 6+ in the dichromate ion to an oxidation number of 3+ in the chromate ion. Therefore, each chromium atom gains three electrons. But since there are two chromium atoms in the dichromate ion, we must think of this half-reaction as gaining six electrons overall. The sulfur atom goes from an oxidation number of 4+ to 6+, so it loses two electrons.
In order to balance the electrons, we need a net transfer of six electrons in each half-reaction. We multiply the ions with the sulfur atoms by three. Note that we also multiply the chromium ion on the right by two to balance the number of Cr atoms:
Cr2O72– + 3 HSO3– → 3 SO42– + 2 Cr3+
The next step is to balance the oxygen atoms. There are 16 oxygen atoms on the left and 12 on the right, so we add 4 water molecules to the right side:
Cr2O72– + 3 HSO3– → 3 SO42– + 2 Cr3+ + 4 H2O
Finally, we balance the hydrogen atoms by adding H+ ions. There are three H atoms on the left and 8 H atoms on the right, so we need five H+ ions on the left:
5 H+ + Cr2O72– + 3 HSO3– → 3 SO42– + 2 Cr3+ + 4 H2O
We check our answer by checking the charge on each side. The left side has charges of 5+ (the H ions), 2- (the dichromate ion) and 3- (the hydrogen sulfite ions) for a net of zero. The right side has charges of 6- (the sulfate ions) and 6+ (the chromate ions) also for a net of zero.
(Look for other tips on this website if you need help with balancing simple redox reactions or redox reactions in basic solutions.)