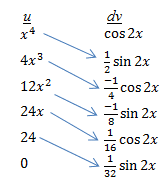Bay Area Tutoring

Solving integrals of the form tan^m x secⁿ x

By Tutor GuyNo Comments

In a recent post, I showed you how to approach integrals of the form

$\displaystyle \int \sin^m{x} \; \cos^n{x} \; dx$

In this post, we look at the similar integral of the form

$\displaystyle \int \tan^m{x} \; \sec^n{x} \; dx$

As before, m and n are integers. The technique we use requires m to be odd or n to be even and we factor out terms of the associated function. We demonstrate with an example. Evaluate:

$\displaystyle \int \tan^5{x} \; \sec^6{x} \; dx$

Here, m is odd and n is even, so we can factor either the tan x or the sec x function. We’ll do it both ways here to show both techniques. First, when m is odd, we factor out a single power of both tan x and sec x and the rest of the integral follows the method we saw in the sin^m x cosⁿx integral example:

$\displaystyle \int \tan^5{x} \; \sec^6{x} \; dx = \int \sec{x} \; \tan{x} \; \tan^4{x} \; \sec^5{x} \; dx =$

$\displaystyle \int \sec{x} \; \tan{x} \; (\tan^2{x})^2 \; \sec^5{x} \; dx = \int \sec{x} \; \tan{x} \; (\sec^2{x} - 1)^2 \; \sec^5{x} \; dx =$

$\displaystyle \int \sec{x} \; \tan{x} \; (\sec^4{x} - 2 \sec^2{x} + 1) \; \sec^5{x} \; dx =$

$\displaystyle \int \sec{x} \; \tan{x} \; (\sec^9{x} -2 \sec^7{x} + \sec^5{x}) \; dx =$

Then letting u = sec x leads to

$\displaystyle f(x) = \frac{1}{10} \sec^{10}{x} - \frac{1}{4} \sec^8{x} + \frac{1}{6} \sec^6{x} + C$

Now let’s do the same integral the other way. When n is even, we factor out a sec² x, and the rest of the process is similar to the first method:

$\displaystyle \int \tan^5{x} \; \sec^6{x} \; dx = \int \sec^2{x} \; \tan^5{x} \; \sec^4{x} \; dx =$

$\displaystyle \int \sec^2{x} \; \tan^5{x} \; (\sec^2{x})^2 \; dx = \int \sec^2{x} \; \tan^5{x}\; (\tan^2{x} + 1)^2 \; dx =$

$\displaystyle \int \sec^2{x} \; \tan^5{x} \; (\tan^4{x} +2\tan^2{x} + 1) \; dx =$

$\displaystyle \int \sec^2{x} (\tan^9{x} + 2 \tan^7{x} + \tan^5{x}) \; dx$

Then letting u=tan x,

$\displaystyle f(x) = \frac{1}{10} \tan^{10}{x} + \frac{1}{4} \tan^8{x} + \frac{1}{6} \tan^6{x} + C$

Wait! That’s not the same integral we got in the method above. Well, actually, it is! After a trig substitution (1 + tan² x = sec² x) and a lot of messy algebra, you can show they are the same function. I’ll leave you to work out the details. Better yet, graph them both on your graphing calculator and you will see they are the same.

Nov 20

Solving integrals of the form sin^m x cosⁿ x when m and n are even

By Tutor GuyNo Comments

In my last post, I showed you the method for integrating functions of the form

$\int \sin^m{x} \; \cos^n{x} \; dx$

when either m or n is odd. If they are both even, the process is more complicated. In this post, I’ll show you how to attack this problem. There are two different methods you can use; if one doesn’t work so well, try the other. We will demonstrate both methods here with an example. Let’s integrate

$\int \sin^2{x} \; \cos^4{x} \; dx$

Method 1

First, rewrite the integral so that the factors are powers of sin²x and cos²x.

$\int \sin^2{x} \; (\cos^2{x})^2 \; dx$

Use the power reducing formulas

$\sin^2{x} = \frac{1}{2}(1- \cos{2x}) \text{ and } \cos^2{x} = \frac{1}{2}(1+\cos{2x})$

to replace both the sin²x and the cos²x terms.

$\displaystyle \int \sin^2{x} \; (\cos^2{x})^2 \; dx = \int \left(\frac{1}{2}(1- \cos{2x})\right) \left(\frac{1}{2} (1+\cos{2x}) \right)^2 \; dx$

Then expand each term and multiply it all out (hey, I said it was more complicated…)

$\displaystyle \int \left(\frac{1}{2}(1- \cos{2x})\right) \left(\frac{1}{2} (1+\cos{2x}) \right)^2 \; dx =$

$\displaystyle \frac{1}{8} \int (1- \cos{2x})(1 + 2 \cos{2x} + \cos^2{2x}) \; dx =$

$\displaystyle \frac{1}{8} \int 1 + 2 \cos{2x} + \cos^2{2x} - \cos{2x} - 2 \cos^2{2x} - \cos^3{2x} \; dx$

$\displaystyle \frac{1}{8} \int 1 + \cos{2x} - \cos^2{2x} - \cos^3{2x} \; dx$

Now we are finally ready to integrate. The first two terms can be integrated by inspection. The third term is attacked by using the power reducing formula. In the last term, the exponent is odd, so apply the technique we used in the last blog post:

$\displaystyle \frac{1}{8} \int 1 + \cos{2x} - \frac{1}{2} (1+\cos{4x}) - \cos{2x}\cos^2{2x} \; dx =$

$\displaystyle \frac{1}{8} \int 1 + \cos{2x} - \frac{1}{2} (1+\cos{4x}) - \cos{2x}(1- \sin^2{2x}) \; dx =$

$\displaystyle \frac{1}{8} \int \frac{1}{2} - \frac{1}{2} \cos{4x} + \cos{2x} \sin^2{2x} \; dx =$

$\displaystyle \frac{1}{8} \left( \frac{1}{2}x - \frac{1}{8} \sin{4x} + \frac{1}{6} \sin^3{2x} \right) + C = \frac{1}{16}x - \frac{1}{64} \sin{4x} + \frac{1}{48} \sin^3{2x} + C$

Whew!

Method 2:

First, rearrange terms so that there is a power of (sin x cos x).

$\displaystyle \int \sin^2{x} \cos^4{x} \; dx = \int \sin^2{x} \cos^2{x} \cos^2{x} \; dx =$

$\displaystyle \int (\sin{x} \cos{x})^2 \cos^2{x} \; dx$

Then use the double angle formula $\sin{x} \cos{x} = \frac{1}{2} \sin{2x}$ and the power reducing formulas as necessary:

$\displaystyle \int (\sin{x} \cos{x})^2 \cos^2{x} \; dx = \int \left(\frac{1}{2} \sin{2x} \right)^2 \left(\frac{1}{2} (1+ \cos{2x}) \right) \; dx$

Expand the terms and multiply out:

$\displaystyle \int \left(\frac{1}{2} \sin{2x} \right)^2 \left(\frac{1}{2} (1+ \cos{2x}) \right) \; dx = \frac{1}{8} \int \sin^2{2x} (1+ \cos{2x}) \; dx =$

$\displaystyle \frac{1}{8} \int \sin^2{2x} + \sin^2{2x} \cos{2x} \; dx = \frac{1}{8} \int \frac{1}{2} (1- \cos{4x}) + \sin^2{2x} \cos{2x} \; dx =$

$\displaystyle \frac{1}{8} \left( \frac{1}{2}x - \frac{1}{8} \sin{4x} + \frac{1}{6} \sin^3{2x} \right) + C = \frac{1}{16}x - \frac{1}{64} \sin{4x} + \frac{1}{48} \sin^3{2x} + C$

Note that this is the same result as in Method 1 above.

Nov 13

Solving integrals of the form sin^m (x) cosⁿ (x)

By Tutor GuyNo Comments

An important class of integrals is of the form:

$\int \sin^m{x} \; \cos^n{x} \; dx$

where m and n are integers. If either m or n is odd, factor out a single power of that function and rewrite the integral to solve with a u substitution. This is best demonstrated with an example:

$\int \sin^5{x} \; \cos^7{x} \; dx$

Here, both m and n are odd, so we can select either function to factor. The process is easier when you pick the smaller of the two exponents, so let’s choose the sin x and we factor out one power as follows:

$\int \sin{x} \; \sin^4{x} \; \cos^7{x} \; dx$

We then rewrite the even power as a power of sin² x so that we can apply a trig identity:

$\int \sin{x} \; \sin^4{x} \; \cos^7{x} \; dx = \int \sin{x} \; (\sin^2{x})^2 \; \cos^7{x} \; dx =$

$\int \sin{x} \; (1-\cos^2{x})^2 \; \cos^7{x} \; dx = \int \sin{x} \; (1-2 \cos^2{x} + \cos^4{x}) \; \cos^7{x} \; dx =$

$\int \sin{x} \; (\cos^7{x} -2 \cos^9{x} + \cos^{11}{x}) \; dx$

This is easily integrated with a u substitution (let u = cos x):

$\dfrac{1}{8} \cos^8{x} - \dfrac{1}{5} \cos^{10}{x} + \dfrac{1}{12} \cos^{12}{x} + C$

So what do you do if both m and n are even? Well, most students just skip the problem and go on to the next one. ☺ But if you want to see the technique, look for my next blog post.

Oct 16

Solving differential equations by separation of variables

By Tutor GuyNo Comments

A common differential equation is of the form $y' = f(x) \cdot g(y)$ . In this situation, the equation can be solved by a technique called “separation of variables”. It involves putting all the y terms on one side of the equation and all the x terms on the other side. Then integration on both sides leads to a solution. Let’s look at a couple of examples.

Example 1

Solve: $\dfrac{dy}{dx} = \dfrac{2x}{y^2}$ with the initial condition $y(0) = 2.$

First, multiply both sides by y²and by dx to separate the variables (all the y terms on one side and all the x terms on the other):

$y^2 \; dy = 2x \; dx$

Note that dy/dx isn’t really a fraction, but you can treat it as a fraction to separate the variables. Now you have an exact differential on each side, so you can integrate both sides:

$\int y^2 \; dy = \int 2x \; dx$

$\dfrac{1}{3} y^3 = x^2 + C$

Why isn’t there a constant of integration on the left side? Well, there was, but we subtracted it and combined it with the constant of integration on the right so there is only one constant. Always do it this way, and put the constant on the independent variable side. Now solve for y:

$y = \sqrt[3]{3x^2 + C}$

Why didn’t we multiply the constant by 3? Well, we did, but a constant times three is still a constant, so we simplified it. Always keep your constant as simple as possible. Now solve for the constant, using the initial condition given:

$2 = \sqrt[3]{3(0)^2 + C} \rightarrow C = 8$

$\therefore y = \sqrt[3]{3x^2 + 8}$

Example 2:

Solve: $\dfrac{dy}{dx} = \dfrac{y}{\sqrt{x}}$ with the initial condition $y(0) = 2.$

As before, separate the variables:

$\dfrac{dy}{y} = \dfrac{dx}{\sqrt{x}}$

Note that the dy and dx terms must always be in the numerator. Now integrate and solve for y:

$\displaystyle \int \dfrac{dy}{y} = \int \dfrac{dx}{\sqrt{x}}$

$\ln |y| = 2 \sqrt{x} + C$

$y = e^{2 \sqrt{x} + C} = Ce^{2 \sqrt{x}}$

Wait, how did the constant move from the exponent to the coefficient? It’s a simplification trick. Proceed as follows:

$y = e^{2 \sqrt{x} + C} = e^{2 \sqrt{x}} \cdot e^C$

But e^C is a constant too, so just call it C. Where did the absolute value sign go? Because C can be either positive or negative, we can drop the absolute value sign around the y. Let’s finish the problem by solving for C:

$2 = Ce^{2 \sqrt{0}} \rightarrow C = 2$

$\therefore y = 2e^{2 \sqrt{x}}$

Oct 09

Tabular integration

By Tutor GuyNo Comments

Occasionally, you will be faced with a complicated integral such as

$\int x^4 \cos 2x \; dx$

If you’ve read some of my other posts, you know that this requires integration by parts. Let’s get started on it and see where it leads.

$\begin{matrix} u = x^4 & dv = \cos 2x \; dx \\ du = 4x^3 \; dx & v = \dfrac{\sin 2x}{2} \end{matrix}$

Then (after a bit of simplifying),

$\int x^4 \cos 2x \; dx = \dfrac{1}{2} x^4 \sin 2x - 2 \int x^3 \sin 2x \; dx$

Now what? Well, the new integral requires integration by parts too! So you go through all the steps again. Then you have to do integration by parts on this result. And again on the next result! It’s tedious, but eventually you get to the correct answer. However, if one of the two functions in the original integral is a polynomial, there is a faster way to do this process. It’s called tabular integration, because all the parts of the integral are found by filling in a table.

Make a two-column table, with the columns labeled u and dv. Put the polynomial function (in our example, x⁴) under the u. Then take the derivative of this function and write it below the original function. Continue taking the derivative until you reach 0. In our example, your first column now looks like this.

$\begin{matrix} \underline{u} & \underline{dv} \\ x^4 & \text{ } \\ 4x^3 & \text{ } \\ 12x^2 & \text{ } \\ 24x & \text { } \\ 24 & \text{ } \\ 0 & \text{ } \end{matrix}$

Next, place the other function in the dv column. Integrate this function repeatedly until there are entries in every row. In our example, your completed table will look like this:

$\begin{matrix} \underline{u} & \underline{dv} \\ x^4 & \cos 2x \\ \text{ } \\4x^3 & \frac{1}{2} \sin 2x \\ \text{ } \\12x^2 & \frac{-1}{4} \cos 2x \\ \text{ } \\24x & \frac{-1}{8} \sin 2x \\ \text{ } \\24 & \frac{1}{16} \cos 2x \\ \text{ } \\0 & \frac{1}{32} \sin 2x \end{matrix}$

You’ve done all the hard work! Now you can write out the integral from the values in this table. First draw an arrow from each u value (except 0) to the dv value on the next line below, as shown here:

Next, place alternating plus and minus signs on each arrow:

Now multiply each u value by the dv value at the other end of the arrow. The plus or minus sign tells you whether to add or subtract this term. For this problem, the integral would be:

$(x^4)(\frac{1}{2} \sin 2x) - (4x^3)(\frac{-1}{4} \cos 2x) + (12x^2)(\frac{-1}{8} \sin 2x) - (24x)(\frac{1}{16} \cos 2x) + (24)(\frac{1}{32} \sin 2x)$

Simplifying gives the final answer (don’t forget the C!):

$\frac{1}{2} x^4 \sin 2x \; + \; x^3 \cos 2x \; - \; \frac{3}{2} x^2 \sin 2x \; - \; \frac{3}{2} \cos 2x \; + \; \frac{3}{4} \sin 2x \; + \; C$

Apr 13

Integrals involving trig substitutions

By Tutor GuyNo Comments

When is it appropriate to solve an integral with a trig substitution? First of all, keep in mind that a trig substitution doesn’t always work. Even when it does work, you are often left with an integral that will require other techniques such as a u substitution or integration by parts. But if you are willing to put in a little effort (and you know your trig identities), trig substitutions allow you to find the antiderivatives of some rather complicated functions.

There are three conditions that you look for—each a radical term of a particular form in the integrand. Each condition is associated with a different substitution. After you make the substitution, you simplify the integrand and go from there.

Term	Substitution	Radical becomes…
$\sqrt{a^2-x^2}$	$\text{Let } x=a \sin \theta; \, dx=a \cos \theta \,d \theta$	$a \cos \theta$
$\sqrt{a^2+x^2}$	$\text{Let } x=a \tan \theta; \, dx=a \sec^2 \theta \,d \theta$	$a \sec \theta$
$\sqrt{x^2-a^2}$	$\text{Let } x=a \sec \theta; \, dx=a \sec \theta \tan \theta \,d \theta$	$a \tan \theta$

Before we look at some example integrals, let’s see why the first radical term above simplifies to $a \cos \theta.$ It’s pretty straightforward if you know your trig identities:

$\sqrt{a^2-x^2}=\sqrt{a^2-(a \sin \theta)^2}= \sqrt{a^2-a^2 \sin^2 \theta}= \sqrt{a^2(1- \sin^2 \theta)} =$

…….. $\sqrt{a^2 \cos^2 \theta} = a \cos \theta$

Example. Integrate the following:

$\text{a.} \displaystyle \int \frac{dx}{\sqrt{1-x^2}} \qquad \text{b.} \int \frac{x^3}{8 \sqrt{4+x^2}}dx \qquad \text{c.} \int x \sqrt{x^2-4} \; dx$

Solutions:

(Does this integral look familiar?) Here, $a=1$ , so use $x= \sin \theta.$ Using the first line of the table above:
…..
$\displaystyle \int \frac{dx}{\sqrt{1-x^2}}= \int \frac{\cos \theta \, d \theta}{\cos \theta}= \int d \theta = \theta +C$
…..
But since $x= \sin \theta, \theta=\sin^{-1} x.$
…..
$\therefore \displaystyle \int \frac{dx}{\sqrt{1-x^2}}=\sin^{-1} x+C$
Here, $a=2$ and we use line 2 from the table above $(x=2 \tan \theta).$ Note that $x^3=8 \tan^3 \theta.$ Upon substitution,
…..
$\displaystyle \int \frac{x^3}{8 \sqrt{4+x^2}}\, dx= \int \frac{8 \tan^3 \theta}{8(2 \sec \theta)}2 \sec^2 \theta \, d \theta = \int \tan^3 \theta \sec \theta \, d \theta$
…..
Hmm. This is going to take a little bit of extra work… Time to pull out some trig identities:
…..
$\int \tan^3 \theta \sec \theta \, d \theta = \int \tan^2 \theta \tan \theta \sec \theta \, d \theta = \int (\sec^2 \theta -1) \tan \theta \sec \theta \, d \theta$
…..
Now a u substitution, letting $u= \sec \theta$ :
…..
$\displaystyle \int (u^2-1) \, du= \frac{1}{3} u^3-u+C= \frac{1}{3} \sec^3 \theta - \sec \theta +C$
…..
How do we get our answer back in terms of $x?$ Draw a triangle that shows how $x$ and $\tan \theta$ are related, then use the Pythagorean theorem to find an expression for $\sec \theta.$ In the triangle below,
…..
$x=2 \tan \theta \therefore \sec \theta = \dfrac{\sqrt{4+x^2}}{2}$
Substitute into the integral above to get:
$\displaystyle \int \frac{x^3}{8 \sqrt{4+x^2}} dx=\frac{1}{3} \sec^3 \theta - \sec \theta +C= \frac{(4+x^2)^{3/2}}{24}- \frac{(4+x^2)^{1/2}}{2}+C$

This can be simplified further by factoring:
…..
$\displaystyle \int \frac{x^3}{8 \sqrt{4+x^2}}dx= \frac{(4+x^2)^{3/2}}{24}- \frac{(4+x^2)^{1/2}}{2}+C= \frac{1}{24}(x^2-8) \sqrt{4+x^2}$
…..
Whew!
This is a trick question. Even though it fits the condition given in the table (and you could integrate with a trig substitution if you wanted), it’s easier to do this one with a u substitution: $u=x^2-4$ and $du=2x \; dx:$
…..
$\displaystyle \int x \sqrt{x^2-4} \, dx= \frac{1}{2} \int \sqrt{u} \, du= \frac{1}{3}u^{3/2}+C= \frac{1}{3}(x^2-4)^{3/2}+C$

The lesson here is to look for u substitutions before you look for trig substitutions.

Apr 06

Using f”(x) to interpret f’(x)

By Tutor GuyNo Comments

You know that the second derivative of a function is used to characterize the concavity of the function. But did you know that the second derivative also gives you information about the first derivative? Well, of course it does, because the second derivative is the first derivative of the first derivative. To put it simply, when the second derivative is positive, that means the first derivative is increasing. When the second derivative is negative, the first derivative is decreasing.

But wait, I thought when the second derivative is positive, that means the original function is concave up! Well, yes, that’s true too. So that means wherever a function is concave up, its first derivative is increasing. And wherever a function is concave down, the first derivative is decreasing.

This is another way you can analyze the behavior of a function.

Feb 23

u substitutions with definite integrals

By Tutor GuyNo Comments

When a definite integral requires a u substitution to solve, be sure to substitute for the limits of integration as well. This way, you don’t need to substitute back in for the original function. Instead, you evaluate the integral using the new (u) limits. Here’s an example to show how this works.

Evaluate:

$\displaystyle \int_0^{\pi/4} \sec^2 \theta \tan^2 \theta \; d \theta$

This is an obvious candidate for a u substitution. (See other posts on this website for more information on when to use u substitutions.)

Let $u= \tan \theta$ . Then $du=\sec^2 \theta \; d \theta$ .

But don’t stop there! Use your expression for u to determine the new limits as well.

$\theta =0 \rightarrow u=0; \; \theta= \dfrac{\pi}{4} \rightarrow u=1$

So the new integral becomes

$\displaystyle \int_0^{\pi/4} \sec^2 \theta \tan^2 \theta \; d \theta =\int_0^1 u^2 \; du= \left. \dfrac{1}{3}u^3 \right |_0^1=\dfrac{1}{3}-0=\dfrac{1}{3}$

You have found the solution to the original integral without needing to put the integral back in terms of $\theta$ .

Jan 12

How to approach integration by parts

By Tutor GuyNo Comments

In an earlier post, I described a strategy for approaching integrals and how to decide what technique to use. One question I suggested you ask yourself is “Can I use integration by parts?” In this post, I describe how you decide when integration by parts is the right approach, and how you decide which term will be u and which will be dv.

There is no product rule for integrals, but when you see an integrand that is the product of two functions [and u substitution has been ruled out], integration by parts is often the right approach. For example, each of the following integrals should be solved using integration by parts:

$\displaystyle \int x^2e^x \; dx \\ \displaystyle \int e^x \sin x \; dx \\ \displaystyle \int x \tan^{-1} x \; dx$

Once you decide that integration by parts is the correct technique, does it matter which factor you make u and which you make dv? Usually, yes. But don’t worry if you make the wrong choice—you’ll know that pretty quickly. Remember that the purpose of integration by parts is to take a complicated integrand and make it simpler. If you choose your u and dv incorrectly, your integrand will get more complicated. When you find your integral getting worse, just start again and switch your choices for u and dv. (If switching choices doesn’t make your integral look better, perhaps integration by parts isn’t the proper technique for the integral.)

Here’s a trick to help you decide which factor should be the u term: LIPET. This is a mnemonic to help you determine the priority for assigning factors to be u. The acronym stands for the following:

L: logarithmic functions
I: inverse trigonometric functions
P: polynomials
E: exponential functions
T: trigonometric functions

For example, the first integral above is the product of a polynomial and an exponential function. P precedes E in LIPET, so make x² the u term and e^x the dv term. The third integral above is the product of a polynomial and an inverse trig function, so let tan^-1x be the u term and x will be the dv term.

Finally, note that even though integration by parts creates a simpler integral, it won’t always create an integral you can evaluate by inspection. Often, you will need to use another technique to integrate the new integrand, or perhaps you will need to do integration by parts a second time.

Jan 05

Strategies for finding integrals

By Tutor GuyNo Comments

How does one become an “expert integrator”? There are a lot of integration techniques, and recognizing which technique is the best is the first step to finding the integral. Many new calculus students look at an integral and don’t even know where to start. Here is a strategy you can adopt when faced with an integral. Carry on this internal dialog with yourself:

Is this something that I can integrate by inspection?
Is this an integral that can be turned into an elementary integral by simplifying?
Is there a trig identity that will simplify the integral?
Is it a candidate for a u substitution?
Can I use integration by parts?
Will decomposition by partial fractions be useful?
Does the integral involve a product of trig functions?
Would a trig substitution be effective?
Can I find it in a table of integrals?

Yes, this is a long list. But with practice, you can work your way through it pretty quickly. [If you are taking Calc AB this year, you will only learn the first four or five steps.] Think of each integration technique as a tool for your toolbox; with each integral you encounter, you decide which tool is the best for that problem.

Let’s look at a couple of examples to see how this works.

Example 1. Evaluate:

$\displaystyle \int {\sec}^2 x+x^2-2x \; dx$

This is an integral consisting of only elementary derivatives, so you can integrate it by inspection:

$\displaystyle \int {\sec}^2 x+x^2-2x \; dx = \tan x+ \dfrac{1}{3}x^3-x^2+C$

Note that you need to know the derivatives of the elementary functions in order to recognize when you can integrate by inspection. This means the derivatives of the trig functions, exponential and log functions and the inverse trig functions, not just polynomials.

Example 2. Evaluate:

$\displaystyle \int (x^2-1)(2x^2+3x) \; dx$

This is not an elementary derivative, so it cannot be integrated by inspection. But the integrand can by simplified by multiplying the terms out, turning it into an elementary derivative:

$\displaystyle \int (x^2-1)(2x^2+3x) \; dx \displaystyle \int 2x^4+3x^3-2x^2-3x \; dx=\dfrac{2}{5}x^5+\dfrac{3}{4}x^4-\dfrac{2}{3}x^3- \dfrac{3}{2}x^2+C$

Example 3. Evaluate:

$\displaystyle \int \tan^2 x \; dx$

This is not an elementary derivative. Is there a trig identity that will help? Yes, use the following Pythagorean identity to turn this into a simple integral:

$\displaystyle \int \tan^2 x \; dx = \displaystyle \int \sec^2 x-1 \; dx = \tan x-x+C$

At this point, you might be thinking “how am I supposed to see that identity?” Well, there’s no substitute for experience and practice. It’s important to know your basic trig identities, so you can rewrite a trig integral in a different form. If one identity doesn’t work, try another. Finding integrals is as much an art as it is a science. Be creative and be inventive.

(Look for other tips on integral problems on this website for strategies on u substitution, integration by parts, products of trig functions and trig substitutions.)

Archive

For the Calculus category

Solving integrals of the form tan^m x secⁿ x

Solving integrals of the form sin^m x cosⁿ x when m and n are even

Solving integrals of the form sin^m (x) cosⁿ (x)

Solving differential equations by separation of variables

Tabular integration

Integrals involving trig substitutions

Using f”(x) to interpret f’(x)

u substitutions with definite integrals

How to approach integration by parts

Strategies for finding integrals

Tutor Guy Homework Tips