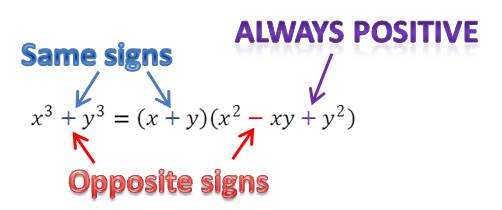
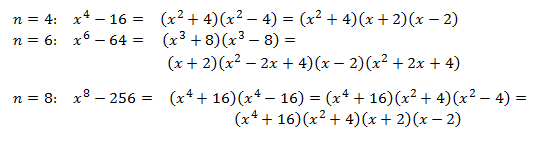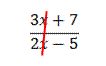Bay Area Tutoring

Factoring ax² + bx + c, part 2

By Tutor GuyNo Comments

In my last post, I showed you a procedure for how to factor a quadratic when the leading coefficient is not equal to 1. Here I refine that method slightly with a short cut that makes your work even quicker. However, this method is a bit more difficult—if you are not really good at mental calculations, you will need to practice this a few times to get it down. To compare methods, I’ll use the same quadratic we factored in the last post.

Problem: Factor $12x^2+4x-5$

Our first step is the same as in the previous method—we need to find two numbers that multiply together to give $60$ (that’s $12*-5$ ) and add together to give $+4$ . Of course, those numbers are the same as they were in the last post: $+10$ and $-6$ .
……
Now here’s the shortcut. Divide both of these numbers by the leading coefficient, $12$ . That gives two fractions:
…..
….. $\dfrac{10}{12} \;\; \text{and } \dfrac{-6}{12}$
…..
Next, simplify the fractions if possible. In our example, we get
…..
….. $\dfrac{5}{6} \;\; \text{and } \dfrac{-1}{2}$
…..
In each fraction, the denominator is the coefficient of the x term in our factor and the numerator is the constant term. So our two factors must be $6x+5$ and $2x-1$ . See the diagram below:

Feb 09

Factoring ax² + bx + c

By Tutor GuyNo Comments

You probably have a lot of experience factoring quadratics of the form $x^2+bx+c$ . (That is, where $a$ , the coefficient on the $x^2$ term is equal to $1$ .) But what do you do when $a$ isn’t $1$ ? For example, let’s factor $12x^2+4x-5$ . You may have been taught a trial-and-error technique where you look for all the numbers that multiply to give $12x^2$ and combine them with all the numbers that multiply to give $5$ and test each one to see which gives the correct middle term. But there’s a simple algorithm that takes all the guesswork out. I’ll show you the procedure with an example.

Problem: Factor $12x^2+4x-5$

Similar to the case where $a=1$ , look for two numbers that multiply together to give $a \cdot c$ (in our example, $12 \cdot -5=-60$ ) and add together to give $b$ (i.e., $+4$ in our example). [Actually, you can see that this is just like the $a=1$ case, because there you were looking for two numbers that multiply together to give $c$ , but when $a=1$ , $a \cdot c=c$ …] For our example, those numbers are $+10$ and $-6 \\$ .
…..
Bring down the first term without changing it:
…..
….. $12x^2$
…..
Write the linear term as a sum or difference using the two numbers you found in step A.:
…..
….. $12x^2$ $+10x-6x$
…..
(Don’t worry about which term comes first. As it turns out, you can write these two terms in either order.)
…..
Bring down the last term without changing it:
…..
….. $12x^2$ $+10x-6x$ $- \; 5$
…..
Now comes the magic. Look at the first two terms only from step D (cover up the last two terms if that helps you) and factor them:
…..
….. $2x$ $\!\!(6x+5)$
…..
Now look at the last two terms in step D (again, cover the first two terms if that helps you) and factor them. And this is very important: if the $x$ term has a minus sign on it, always factor out the minus sign:
…..
….. $2x$ $\!\! (6x+5)$ $- \; 1$ $\!\! (6x+5)$
…..
(Note that if nothing factors out of the last two terms, write a $1$ (you can always factor $1$ out of any term).
…..
Are the two expressions in the parentheses the same? They have to be. If they’re not, you’ve done something wrong. That’s one of the factors in your answer. The other factor is made up of the numbers outside the parentheses:
…..
….. $(2x-1)$ $\!\! (6x+5)$

Tada! I’ll leave it to you to show that if you had written the linear terms in step C in the reverse order, you’d get the same answer.

Dec 08

Factoring sums and differences of fifth powers (and higher!) when the power is odd

By Tutor GuyNo Comments

Occasionally, you are required to factor a polynomial that is in the form of a sum or difference of two power terms (i.e., xⁿ– yⁿ). In my last post, I showed you a simple procedure you can learn to help you factor the binomial if the value of the power is 4 or greater and the power is even. [If you are reading this post, you should already be familiar with factoring the difference of two squares and the difference of two cubes. Check this website for posts on those procedures.] In this post, I show you a procedure (more complicated than the others, I admit) that you can use to factor these binomials when the power is odd.

First, let’s see how this works on some examples:

Do you see the pattern? When factoring aⁿ– bⁿ or aⁿ+ bⁿ (for n odd), there is always a linear term a ± b, where the plus or minus sign is the same as in the original binomial. The remaining factor is a little more complicated, but it does have a simple pattern. Each term consists of the first term in the binomial (with its exponent decreasing from n – 1 to 0) and the second term in the binomial with its exponent increasing from 0 to n – 1. In the first example above, the x term decreased from x⁴ to x⁰. The 2 term increased from 2⁰ to 2⁴. If you started with the difference of two powers, all of the signs in the second factor are plus signs. If you started with the sum of the two powers, the first sign in the second factor is a minus sign and the signs alternate after that.

Dec 01

Factoring differences of fourth powers (and higher!) when the power is even

By Tutor GuyNo Comments

Occasionally, you are required to factor a polynomial that is in the form of a difference of two power terms (i.e., xⁿ – yⁿ). There is a simple procedure you can learn to help you factor the polynomial if the value of the power is 4 or greater and the power is even. [If you are reading this post, you should already be familiar with factoring the difference of two squares and the difference of two cubes. Check this website for posts on those procedures.]

First, let’s see how this works on some examples:

You can see that whenever the power is even, you treat the binomial as the difference of two squares and find its factors. If the factors are still the sum and difference of perfect squares, you repeat the process with the term that is the difference of two squares. If the factors are now the sum and difference of perfect cubes, you follow the method for factoring the sum or difference of two cubes. If the powers are sums and differences of odd powers higher than 3, there is another procedure to factor them. You can find another post on this website that shows that procedure.

Sep 15

Factoring the difference of two squares

By Tutor GuyNo Comments

You will spend a lot of time in algebra (and courses beyond) factoring polynomials into linear and quadratic terms. There are some special polynomials that occur so frequently that you should recognize them on sight so that you know the method for factoring them. The most common is the binomial of the form $a^2-b^2$ . This is called the difference of two squares because both terms are perfect squares and you are subtracting (finding the difference between) the two terms.

Some examples of this binomial are $x^2-4$ , $9x^4-16y^2$ and $121y^2z^2-25w^4a^6b^{12}$ . Note that in each case, both terms are perfect squares.

It is very easy to factor these expressions—you can do it by inspection. The rule is simple and you must memorize it: $a^2-b^2=(a+b)(a-b)$ . Once you determine that an expression is the difference of two squares, you can write out its factors immediately. Let’s see how it works with the three examples given above:

$x^2-4=(x+2)(x-2)$

$9x^4-16y^2=(3x^2+4y)(3x^2-4y)$

$121y^2z^2-25w^4a^6b^{12}=(11yz+5w^2a^3b^6)(11yz-5w^2a^3b^6)$

It’s really that easy once you learn the format. Of course it doesn’t matter what order you write the two factors, so $x^2-4=(x-2)(x+2)$ is also correct.

One other important point: this factoring rule works in reverse, too! If you have to distribute (multiply out) two factors and you see they are in the form of $(a+b)(a-b)$ , you should recognize that this gives the difference of two squares: $a^2-b^2$ . You can do this immediately, without multiplying out every term. Learning this formula will save you lots of time.

Jul 21

The Most Common Factoring Mistake

By Tutor GuyNo Comments

I am surprised (and a little disappointed) every year when one of my students tries to simplify a polynomial fraction by cancelling out terms that can’t be cancelled out. For example, when faced with

$\dfrac{3x+7}{2x-5}$

inevitably, a student will ask me, “Can I cancel out the x’s like this?”

Tears well up in my eyes as I explain that no, the x’s do not cancel. I explain patiently why the x’s do not cancel. And very often, the next time I work with that student, he or she will try to cancel out the x’s again. This is the most common factoring mistake I see students make, and it’s not limited to Algebra students. I’ve even seen Calculus student make this error. That usually makes me sob quite loudly.

If you would like to keep me from crying, then you need to learn how to simplify polynomial fractions. It’s quite simple once you understand that terms that are added do not cancel out. Only factors that are multiplied together can cancel. Let’s start by looking at a fraction with numbers and no variables.

$\dfrac{210}{462}$

Can this be simplified? Of course. Most students will divide the top and bottom by 2, then by 3, and then by 7, as follows:

$\dfrac{210}{462}=\dfrac{105}{231}=\dfrac{35}{77}=\dfrac{5}{11}$

This is correct. But why can you cancel out a 2 and a 3 and a 7? It’s because they are factors of the numerator and the denominator. Let’s do the same problem by completely factoring the top and bottom first:

$\dfrac{210}{462}=\dfrac{2\cdot 3 \cdot 5 \cdot 7}{2 \cdot 3 \cdot 7 \cdot 11}=\dfrac{5}{11}$

When you write it out like this, you can see that the 2’s cancel, the 3’s cancel, and the 7’s cancel. And they cancel only because they are factors.

Now let’s try to simplify some polynomial fractions. Start by factoring the numerator and denominator completely, then any like factors will cancel:

$\dfrac{2x-4}{6x+14}=\dfrac{2(x-2)}{2(x+7)}=\dfrac{x-2}{x+7}$

$\dfrac{4x+8}{12x+24}=\dfrac{4(x+2)}{12(x+2)}=\dfrac{4}{12}=\dfrac{1}{3}$

$\dfrac{x^2-1}{x^2+4x+3}=\dfrac{(x+1)(x-1)}{(x+1)(x+3)}=\dfrac{x-1}{x+3}$

Oct 24

Factoring the sum or difference of two cubes

By Tutor GuyNo Comments

The sum or difference of two cubes can always be factored as follows:

$(x^3+y^3)=(x+y)(x^2-xy+y^2)$

$(x^3-y^3)=(x-y)(x^2+xy+y^2)$

These formulas are not too easy to figure out on your own, so your best approach is to memorize them. But how do you keep straight where the plus and minus signs go? Some students like to use the acronym “SOAP”, which stands for Same-Opposite-Always Positive. This means that the first sign is the same as the sign in the sum or difference of the cubes, the second sign is the opposite of this sign, and the third sign is always positive.

Aug 08

The zero property

By Tutor GuyNo Comments

Perhaps the most important property you’ll learn in Algebra 1 is the zero property.

It says that if a · b = 0, then either a = 0 or b = 0 (or both).

This property allows us to solve most of the equations we encounter in algebra and beyond. First, move everything to one side of the equation (so the other side equals 0). Second, factor the equation. Then we can set each factor equal to zero and solve.

You will use this technique (on more and more complicated equations) in every math class you take.

Example: Solve x² = 3x.

Solution:

x² – 3x = 0	(Move everything to one side.)
x(x-3) = 0	(Factor.)
x = 0 or x-3 = 0	(Set each factor equal to 0.)
x = 0 or x = 3	(Solve each factor.)

Archive

Factoring ax² + bx + c, part 2

Factoring ax² + bx + c

Factoring sums and differences of fifth powers (and higher!) when the power is odd

Factoring differences of fourth powers (and higher!) when the power is even

Factoring the difference of two squares

The Most Common Factoring Mistake

Factoring the sum or difference of two cubes

The zero property

Tutor Guy Homework Tips