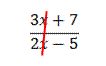I am surprised (and a little disappointed) every year when one of my students tries to simplify a polynomial fraction by cancelling out terms that can’t be cancelled out. For example, when faced with
inevitably, a student will ask me, “Can I cancel out the x’s like this?”
Tears well up in my eyes as I explain that no, the x’s do not cancel. I explain patiently why the x’s do not cancel. And very often, the next time I work with that student, he or she will try to cancel out the x’s again. This is the most common factoring mistake I see students make, and it’s not limited to Algebra students. I’ve even seen Calculus student make this error. That usually makes me sob quite loudly.
If you would like to keep me from crying, then you need to learn how to simplify polynomial fractions. It’s quite simple once you understand that terms that are added do not cancel out. Only factors that are multiplied together can cancel. Let’s start by looking at a fraction with numbers and no variables.
Can this be simplified? Of course. Most students will divide the top and bottom by 2, then by 3, and then by 7, as follows:
This is correct. But why can you cancel out a 2 and a 3 and a 7? It’s because they are factors of the numerator and the denominator. Let’s do the same problem by completely factoring the top and bottom first:
When you write it out like this, you can see that the 2’s cancel, the 3’s cancel, and the 7’s cancel. And they cancel only because they are factors.
Now let’s try to simplify some polynomial fractions. Start by factoring the numerator and denominator completely, then any like factors will cancel: