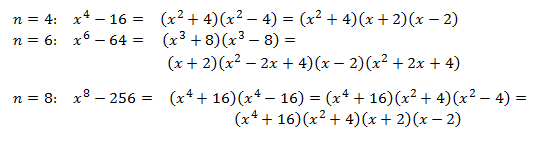Archive

Dec 08

Factoring sums and differences of fifth powers (and higher!) when the power is odd

By Tutor GuyNo Comments

 

Occasionally, you are required to factor a polynomial that is in the form of a sum or difference of two power terms (i.e., xn – yn). In my last post, I showed you a simple procedure you can learn to help you factor the binomial if the value of the power is 4 or greater and the power is even. [If you are reading this post, you should already be familiar with factoring the difference of two squares and the difference of two cubes. Check this website for posts on those procedures.] In this post, I show you a procedure (more complicated than the others, I admit) that you can use to factor these binomials when the power is odd.

First, let’s see how this works on some examples:

 

 

 

 

Do you see the pattern? When factoring an – bn or an + bn (for n odd), there is always a linear term a ± b, where the plus or minus sign is the same as in the original binomial. The remaining factor is a little more complicated, but it does have a simple pattern. Each term consists of the first term in the binomial (with its exponent decreasing from n – 1 to 0) and the second term in the binomial with its exponent increasing from 0 to n – 1. In the first example above, the x term decreased from x4 to x0. The 2 term increased from 20 to 24. If you started with the difference of two powers, all of the signs in the second factor are plus signs. If you started with the sum of the two powers, the first sign in the second factor is a minus sign and the signs alternate after that.

Dec 01

Factoring differences of fourth powers (and higher!) when the power is even

By Tutor GuyNo Comments

 

Occasionally, you are required to factor a polynomial that is in the form of a difference of two power terms (i.e., xn – yn). There is a simple procedure you can learn to help you factor the polynomial if the value of the power is 4 or greater and the power is even. [If you are reading this post, you should already be familiar with factoring the difference of two squares and the difference of two cubes. Check this website for posts on those procedures.]

First, let’s see how this works on some examples:

 

 

 

 

 

 

You can see that whenever the power is even, you treat the binomial as the difference of two squares and find its factors. If the factors are still the sum and difference of perfect squares, you repeat the process with the term that is the difference of two squares. If the factors are now the sum and difference of perfect cubes, you follow the method for factoring the sum or difference of two cubes. If the powers are sums and differences of odd powers higher than 3, there is another procedure to factor them. You can find another post on this website that shows that procedure.

Sep 15

Factoring the difference of two squares

By Tutor GuyNo Comments

 

You will spend a lot of time in algebra (and courses beyond) factoring polynomials into linear and quadratic terms. There are some special polynomials that occur so frequently that you should recognize them on sight so that you know the method for factoring them. The most common is the binomial of the form a^2-b^2. This is called the difference of two squares because both terms are perfect squares and you are subtracting (finding the difference between) the two terms.

Some examples of this binomial are x^2-4, 9x^4-16y^2 and 121y^2z^2-25w^4a^6b^{12}. Note that in each case, both terms are perfect squares.

It is very easy to factor these expressions—you can do it by inspection. The rule is simple and you must memorize it: a^2-b^2=(a+b)(a-b). Once you determine that an expression is the difference of two squares, you can write out its factors immediately. Let’s see how it works with the three examples given above:

x^2-4=(x+2)(x-2)

9x^4-16y^2=(3x^2+4y)(3x^2-4y)

121y^2z^2-25w^4a^6b^{12}=(11yz+5w^2a^3b^6)(11yz-5w^2a^3b^6)

It’s really that easy once you learn the format. Of course it doesn’t matter what order you write the two factors, so x^2-4=(x-2)(x+2) is also correct.

One other important point: this factoring rule works in reverse, too! If you have to distribute (multiply out) two factors and you see they are in the form of (a+b)(a-b), you should recognize that this gives the difference of two squares: a^2-b^2. You can do this immediately, without multiplying out every term. Learning this formula will save you lots of time.

Blue Taste Theme created by Jabox