Solid figures can be scary for a lot of students. There are a lot of confusing formulas and it can be difficult to draw a three-dimensional figure on a flat sheet of paper. But solids can be tamed if you categorize them by the number of bases. Note in the table below that the formulas for prisms and cylinders are exactly the same, as are the formulas for pyramids and cones. You will have the most success if you memorize these formulas—then you just plug in the given values to find the unknown values. If you are struggling with the formulas, print this page out and paste it into your binder until you are more comfortable with them.
|
Bases |
Figure | Lateral surface area | Volume |
|
2 |
Prism | ||
| Cylinder | |||
|
1 |
Pyramid | ||
| Cone | |||
|
0 |
Sphere |
p = perimeter; h = height; ℓ = slant height; B = Base area; r = radius
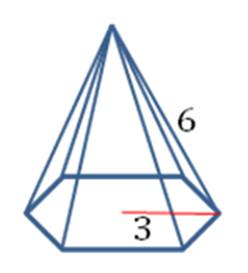
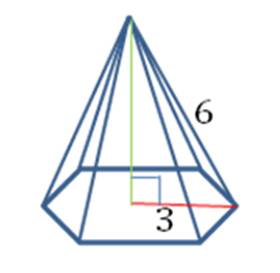
An added wrinkle that can make pyramids difficult is that you are not always given all the necessary information to plug into the formulas. What do you do? Remember what you’ve learned about regular polygons and use the Pythagorean Theorem! Let’s look at an example. The pyramid in the figure is a regular pyramid with a hexagonal base. The edge length is 6 cm and the radius of the base is 3 cm. Find the lateral surface area and the volume of the pyramid.
You can see from the pyramid formulas above that we need to know the perimeter of the base and the slant height to find the area, and we need to know the Base area and the height to find the volume. And we don’t have any of these numbers! It seems like we don’t have enough information. But there was one other clue that will help us solve this puzzle. The pyramid is regular, which means the foot of the altitude touches the center of the base, and the base is regular. If you draw the altitude, it forms a right triangle with the radius and the edge.
Using the Pythagorean Theorem (or recognizing this as a 30°-60°-90° triangle), you can easily find the altitude is
Because the base is a regular hexagon, you can also find the edge length, perimeter and the apothem:
Finally, the triangle formed by the altitude, apothem and slant height is also a right triangle.
From the Pythagorean Theorem again, we find the slant height:
Now we have all the information we need to find the area and volume. Just plug it all in:
Whew! Yes, that’s a lot of work, but just break the problem down piece by piece and you can solve these problems like a pro!