Archive

Mar 09

Using force and torque to solve motion problems

By Tutor GuyNo Comments

 

When solving motion problems in physics, start by drawing a picture of the situation. Then use the picture to create an FBD. If there are no rotations, set the linear forces equal to ma and solve. If there are rotations, set the linear forces equal to ma and set all the torques equal to I \alpha. Then solve the equations.

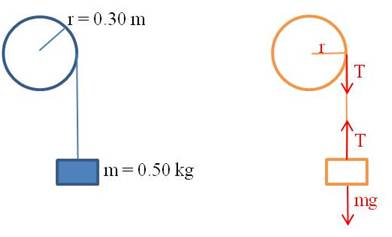
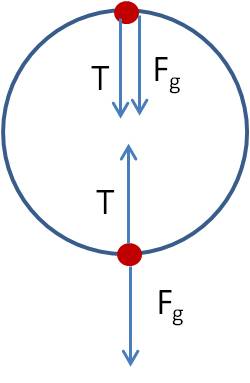
Example 1: A block of mass 0.50 \, kg is attached to the end of a string of negligible mass wrapped around a wheel of radius 0.30 \, m as shown. If the wheel has a moment of inertia of 0.18 \, kg \cdot m^2, find the acceleration of the mass as it falls.

 

 

 

 

 

 

 

 

We can find all the information we need by writing the linear and rotational equations of force. The block is experiencing only linear motion, so there is one equation for it. The two forces acting on it are gravity and the tension in the string:

mg-T=ma

The wheel is experiencing only rotational motion, so there is only one equation for it too. The only torque acting on the wheel is due to the tension in the string:

\tau=F \cdot r=Tr=I \alpha

It appears at first as though there are too many unknowns: T, a, \text{ and } \alpha. But remember that a=r \alpha. So we can write the second equation as:

Tr=I \alpha =I \dfrac{a}{r}

 Solve both equations for T and substitute:

mg-ma=I \dfrac{a}{r^2} \rightarrow mg=I \dfrac{a}{r^2}+ma

\therefore a= \dfrac{mg}{\dfrac{I}{r^2}+m}= \dfrac{0.50 \cdot 9.8}{\dfrac{0.18}{0.30^2}+0.50}=2.0 \, m/s^2

 

Mar 02

When is torque useful in an equilibrium problem?

By Tutor GuyNo Comments

 

When you are trying to find a particular force for a system in equilibrium, you draw an FBD and set the sum of all the forces equal to zero. But sometimes, this doesn’t provide enough information for you to calculate the missing value. For example, check this problem out:

Example: A 6 m bench is supported by two posts at its two ends. The bench is a uniform piece of wood with a weight of 200 N. A dog with a weight of 100 N sits 2 m from one end of the bench. Find the magnitudes of the forces exerted on the bench by the two supports.

 

 

 

 

 

 

 

 

Solution: If we start by drawing a schematic of the bench, we can attach all the forces:

 

 

 

 

 

 

Obviously, the four forces sum to zero—the two support forces pushing up balance the weight of the bench and the dog. But that only gives us one equation and we have two unknowns—the forces upward by each leg of the bench.

How do we solve the problem? We recognize that the sum of all the torques also equals zero. But if the bench is not rotating, what’s the pivot point? We can use any point we want! Let’s pick the left end of the bench, because then the force from the left support does not exert a torque. There are then two clockwise torques (the center of mass of the bench and the dog) and one counterclockwise torque (the right leg of the bench). Now we have two equations:

F_1+F_2-F_{bench}-F_{dog}=F_1+F_2-200-100=0

\tau_{bench}+\tau_{dog}-\tau_2=(200)(3)+(100)(4)-(F_2)(6)=0

\therefore F_2=167 \, N \text{ and } F_1=133 \, N

Note that we could have chosen any other point along the bench as our pivot point, and we would have obtained the same result.

Nov 24

Using ratios to solve physics problems when variables change values

By Tutor GuyNo Comments

 

A common question when you learn an equation in physics is “how is the value of one variable affected when a second variable is changed?” For example, “An astronaut has a weight of 200 N as she stands on the surface of a certain moon of Jupiter. How much would she weigh standing on a second moon that has three times the mass and twice the radius of the first moon?”

Many students find this a difficult problem to calculate, but it is actually something that you can solve quickly with just a bit of thought. The trick is to recognize that problems of this sort can be solved with a simple ratio. Let’s see how to solve the problem posed above. We will call the astronaut’s weight on the first moon F1 and on the second moon F2. The masses of the two moons are M1 and M2 respectively and their radii are r1 and r2. The mass of the astronaut is MA. Then from the universal law of gravitation:

F_1= \dfrac{GM_1M_A}{r_1^{\; 2}}

 and

F_2= \dfrac{GM_2M_A}{r_2^{\; 2}}

But we are told that the mass of the second moon is three times the mass of the first moon and its radius is twice the radius of the first moon. That means that M2 = 3 M1 and r2 = 2 r1. We substitute these expressions into the equation for F2 above. This gives

F_2= \dfrac{G(3M_1)M_A}{({2r_1)}^2}= \dfrac{3GM_1M_A}{4r_1^{\; 2}}

 Now divide this equation by the first equation and all the variables cancel out:

\dfrac{F_2}{F_1}=\dfrac{\dfrac{3GM_1M_A}{4r_1^{\; 2}}}{\dfrac{GM_1M_A}{r_1^{\; 2}}}=\dfrac{3}{4}

\therefore F_2= \dfrac{3}{4}F_1=150 \; N

With some practice, you will find that you can do many of these problems in your head!

Nov 17

SI unit prefixes

By Tutor GuyNo Comments

Even with scientific notation, very large numbers and very small numbers can be awkward to work with. That is why scientists have developed a set of standard prefixes that are attached to a unit to indicate multiples of that unit. Each of the prefixes represents a particular power of ten. There are currently 24 prefixes in use:

 

Prefixes greater than 1

Factor

Name

symbol

1030

quetta

Q

1027

ronna

R

1024

yotta

Y

1021

zetta

Z

1018

exa

E

1015

peta

P

1012

tera

T

109

giga

G

106

mega

M

103

kilo

k

102

hecto

h

101

deka

da

 

Prefixes less than 1

Factor

Name

symbol

10-1

deci

d

10-2

centi

c

10-3

milli

m

10-6

micro

μ

10-9

nano

n

10-12

pico

p

10-15

femto

f

10-18

atto

a

10-21

zepto

z

10-24

yocto

y

10-27

ronto

r

10-30

quecto

q

 

Do you have to memorize all of these? No. If you are a high school chemistry or physics student, you should know the prefixes in blue above. If you are an AP chemistry or AP physics student, you should also learn the prefixes in red. If you plan to be a scientist or an engineer, it wouldn’t hurt you to learn the rest, but the extreme prefixes are not so common.

Why do the prefixes skip three powers of 10? This allows us to use numbers that are always between 1 and 999. This is easiest to explain with an example. Let’s say we are measuring very small electrical currents. The following table shows how we would state the values without scientific notation, with scientific notation, and with prefixes. You can see how convenient this prefix method is:

Current Scientific notation Prefix notation
0.50 A 5.0 x 10-1 A 500 mA
0.050 A 5.0 x 10-2 A 50 mA
0.0050 A 5.0 x 10-3 A 5 mA
0.00050 A 5.0 x 10-4 A 500 μA
0.000050 A 5.0 x 10-5 A 50 μA
0.0000050 A 5.0 x 10-6 A 5 μA
0.00000050 A 5.0 x 10-7 A 500 nA
0.000000050 A 5.0 x 10-8 A 50 nA
0.0000000050 A 5.0 x 10-9 A 5 nA
0.00000000050 A 5.0 x 10-10 A 500 pA
Sep 08

How to manage projectile motion problems

By Tutor GuyNo Comments

 

In two-dimensional kinematics problems (for example, a ball thrown forward or a missile fired through the air), keep the horizontal (x) and vertical (y) directions separate. The motions in each direction are independent of each other, so you can work them separately.

In the x direction, the velocity will be constant because there is no horizontal force on the object (ignoring air resistance). In the y direction, you need to include the acceleration term due to gravity.

If the object’s initial velocity is not totally horizontal or totally vertical, you need to find the horizontal and vertical components first. If the initial velocity is v_0 and the initial angle is θ, then the two velocity components are:

v_x=v_0 \cos \theta
v_y=v_0 \sin \theta

 

 

 

 

Then the position functions in each direction are as follows:

S_x=v_x t + S_{0x}

S_y=-\frac{1}{2}{}gt^2+v_yt+s_{0y}

 

Jul 28

Storing constants on your graphing calculator

By Tutor GuyNo Comments

 

There are several fundamental constants in physics that you will use over and over. If you get tired of looking them up every time you need one for a calculation, consider storing them in your calculator. The graphing calculator makes it easy to store any value as one of the alphabet letters. It then remains in the calculator until you remove it.

To store a number, type it into the calculator, press the Store key (STO→), then select a letter with the ALPHA key. Then when you need the value, just type the letter on your calculator. Here are the constants I store in my calculator:

Constant letter value
Coulomb law constant k 8.99E9
Elementary charge q 1.60E-19
Planck’s constant h 6.63E-34
speed of light c 2.998E8
Universal gravitation constant G 6.67E-11

 

Other constants you might find useful to store are proton mass, electron mass, vacuum permittivity and permeability, and Boltzmann’s constant.

For example, to calculate the electrical repulsion force between two electrons that are fixed 0.5 m apart, use the equation

\displaystyle F = \frac{kq_{1}q_{2}}{r^2}.

Because the values of k and q are already stored in my calculator, here’s the way this would appear when I crunch it:

ph-1101-const

 

Dec 15

Pulley problems

By Tutor GuyNo Comments

 

In a pulley problem, if you have a chain of boxes all connected by ropes, first find the tension in the rope that goes over the pulley (treat all of the boxes on the table as a single box and all of the boxes hanging down as a single box). Then work your way to each end of the chain one box at a time to find the tension in each rope along the chain.

Example: Find the tensions in each cable and the acceleration of the blocks in the diagram below. Assume that the pulley is massless and the table and pulley are frictionless.

 

 

 

 

 

 

 

 

 

 

 

 

Solution: First, treat the two blocks on the table as a single unit of 5 kg, and treat the two hanging blocks as a single unit of 5 kg:

 

 

 

 

 

 

 

 

 

 

 

 

The net force equation for the “block” on the table is:

T2 = ma = 5a                                (1)

The net force equation for the hanging “block” is:

mg – T2 = ma → 5g – T2 = 5a             (2)

Plugging equation (1) into equation (2) gives

a = g/2 = 4.9 m/s2 and T2 = 5g/2 = 24.5 N.

Now you can find the other tensions. Find T3 by doing an FBD on the 3 kg block:

3g – T3 = 3a = 3g/2

Solve to get T3 = 3g/2 = 14.7 N. Find T1 by doing an FBD on the 4 kg block:

T1 = 4a = 2g, so T1 = 19.6 N.

Dec 12

Solving uniform circular motion problems

By Tutor GuyNo Comments

 

In order for an object to move in a uniform circular path, the net force on the object must be mv2/r. Draw the FBD, and any forces not pointed along a radius of the circle must cancel out.  All the remaining forces must add up to mv2/r.

Example 1: You attach a ball to the end of a rope and swing it around vertically in a circle. If the rope is 0.50 m long, the ball has a mass of 0.50 kg, and the ball is traveling at a constant speed of 6.0 m/s, what is the tension in the rope at the bottom of the circle? At the top of the circle?

Solution: The FBD is shown for the ball at the bottom of the circle and at the top (I’ve shown the ball in its orbit, but left out the rope to make the picture clearer). Let’s solve the bottom case first.

 

 

 

 

 

 

 

 

 

 

 

 

The net force is T– Fg. Since the ball is traveling in a circle, the net force must be the centripetal force that keeps the ball in a circle, so

T-F_g= \dfrac{mv^2}{r} \rightarrow T= \dfrac{mv^2}{r}+mg \rightarrow T= \dfrac{(0.5)(6.0)}{(0.5)}+(0.5)(9.8)=10.9 \, N

 Finding the solution at the top of the circle is just as simple:

T+F_g= \dfrac{mv^2}{r} \rightarrow T= \dfrac{mv^2}{r}-mg \rightarrow T= \dfrac{(0.5)(6.0)}{(0.5)}-(0.5)(9.8)=1.1 \, N

 Note that in problems like this one, the tension is greatest at the bottom and a minimum at the top.

Example 2 : One of the obstacles at your favorite miniature golf course is a loop-the-loop as seen in the picture below. What is the minimum velocity necessary for the golf ball to stay in contact with the loop-the-loop at the top of the loop? The loop has a radius of 1.0 m.

 

 

 

 

 

 

 

Solution: Draw an FBD of the situation.

 

 

 

 

 

 

 

The two forces on the golf ball are the force due to gravity and the normal force of the loop against the golf ball. As in the last example, we set the net force equal to the centripetal force.

F_N+F_g= \dfrac{mv^2}{r}

 You can see from this equation that minimizing the velocity means minimizing the two forces. If the normal force is zero (i.e., if the ball is just barely making contact with the loop, this satisfies our requirement:

0+mg= \dfrac{mv^2}{r} \rightarrow v= \sqrt{rg} \rightarrow v= \sqrt{(1)(9.8)}=3.1 \, m/s

 Note that the answer does not depend on the mass of the golf ball!

Nov 24

Free Body Diagrams when velocity is constant

By Tutor GuyNo Comments

 

Acceleration is the rate of change of the velocity. So if you are told that an object is stationary or is moving at constant velocity, this means the acceleration is zero. From Newton’s Second Law (F = ma), if the acceleration is zero, this means the net force is zero. So whenever velocity is constant, all the forces in the x and y directions must cancel out! Here’s a problem that shows how this concept is a powerful tool for solving free body problems:

Example: Jack pushes a large crate across a level surface at a constant speed. The crate has a mass of 50 kg and Jack exerts a horizontal force of 200 N. What is the coefficient of friction, μ?

 

 

 

 

 

 

Answer: It seems that we don’t have enough information because we don’t know the velocity of the crate. But the fact that the speed is constant tells us that the net force is zero. So the solution is straightforward. First draw the free body diagram:

 

 

 

 

 

 

 

 

 

 

 

Because the net force is zero, the weight Fg is equal in magnitude to FN.

F_N=F_g=mg=(50)(9.8)=490 \, N

And because the net force is zero, the force Jack exerts is equal in magnitude to the frictional force.

F_f= \mu F_N=F \rightarrow \mu (490)=200 \rightarrow \mu = 0.41

Nov 21

Finding the angles of the gravity components in a ramp problem

By Tutor GuyNo Comments

 

In a ramp (or inclined plane) problem, the angle of the ramp is the same as the angle the gravity vector makes with the component normal to the ramp.

 

 

 

 

 

 

 

 

Here’s how you can be sure this is true: Look at the component of the gravity vector that is perpendicular to the ramp. Imagine that the ramp is horizontal—that is, θ is currently 0. Then the perpendicular component points straight down so that it coincides with Fg. Now start lifting the ramp. As the ramp angle increases, so does the angle between the perpendicular component and the gravity vector. You can see that these two angles have to be the same.

< Older
Blue Taste Theme created by Jabox