When you are trying to find a particular force for a system in equilibrium, you draw an FBD and set the sum of all the forces equal to zero. But sometimes, this doesn’t provide enough information for you to calculate the missing value. For example, check this problem out:
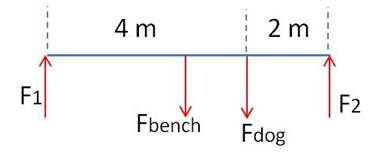
Example: A 6 m bench is supported by two posts at its two ends. The bench is a uniform piece of wood with a weight of 200 N. A dog with a weight of 100 N sits 2 m from one end of the bench. Find the magnitudes of the forces exerted on the bench by the two supports.
Solution: If we start by drawing a schematic of the bench, we can attach all the forces:
Obviously, the four forces sum to zero—the two support forces pushing up balance the weight of the bench and the dog. But that only gives us one equation and we have two unknowns—the forces upward by each leg of the bench.
How do we solve the problem? We recognize that the sum of all the torques also equals zero. But if the bench is not rotating, what’s the pivot point? We can use any point we want! Let’s pick the left end of the bench, because then the force from the left support does not exert a torque. There are then two clockwise torques (the center of mass of the bench and the dog) and one counterclockwise torque (the right leg of the bench). Now we have two equations:
Note that we could have chosen any other point along the bench as our pivot point, and we would have obtained the same result.