Mar 09

Using force and torque to solve motion problems

By Tutor GuyNo Comments

 

When solving motion problems in physics, start by drawing a picture of the situation. Then use the picture to create an FBD. If there are no rotations, set the linear forces equal to ma and solve. If there are rotations, set the linear forces equal to ma and set all the torques equal to I \alpha. Then solve the equations.

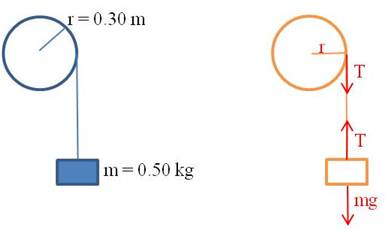
Example 1: A block of mass 0.50 \, kg is attached to the end of a string of negligible mass wrapped around a wheel of radius 0.30 \, m as shown. If the wheel has a moment of inertia of 0.18 \, kg \cdot m^2, find the acceleration of the mass as it falls.

 

 

 

 

 

 

 

 

We can find all the information we need by writing the linear and rotational equations of force. The block is experiencing only linear motion, so there is one equation for it. The two forces acting on it are gravity and the tension in the string:

mg-T=ma

The wheel is experiencing only rotational motion, so there is only one equation for it too. The only torque acting on the wheel is due to the tension in the string:

\tau=F \cdot r=Tr=I \alpha

It appears at first as though there are too many unknowns: T, a, \text{ and } \alpha. But remember that a=r \alpha. So we can write the second equation as:

Tr=I \alpha =I \dfrac{a}{r}

 Solve both equations for T and substitute:

mg-ma=I \dfrac{a}{r^2} \rightarrow mg=I \dfrac{a}{r^2}+ma

\therefore a= \dfrac{mg}{\dfrac{I}{r^2}+m}= \dfrac{0.50 \cdot 9.8}{\dfrac{0.18}{0.30^2}+0.50}=2.0 \, m/s^2

 

Physics
, ,
Blue Taste Theme created by Jabox