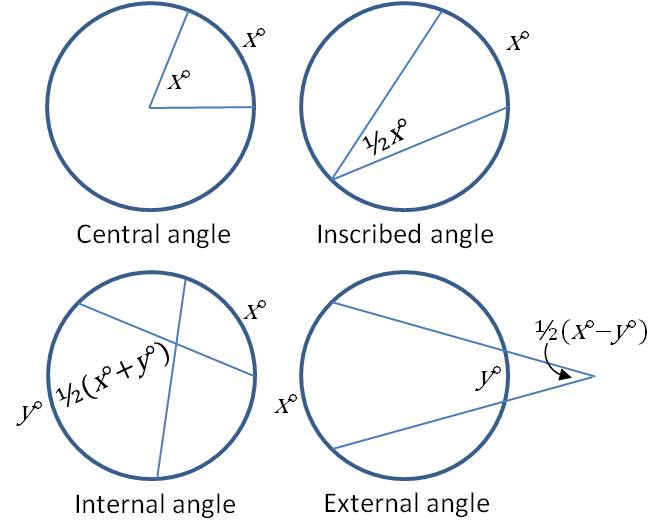
When angles are formed by chords, secants and tangents in a circle, there are several formulas that help you determine the arc measures and angle measures that are formed. With a little bit of thought, you can often find values for all of the arcs and angles around the circle. For many students, the equations are difficult to remember. Your best approach is to categorize the angle by the location of the vertex. Then learn the rule for the angles with that particular vertex. There are four possibilities:
- Central angles: This is an angle whose vertex is at the center of the circle. For all central angles, the angle measure is equal to the arc measure of the subtended arc.
- Inscribed angles: These angles have their vertex on the circle. They can be chord-chord angles or chord-tangent angles. For these angles, the angle measure is one half the arc measure of the subtended arc.
- Internal angles: These are angles whose vertex is in the interior of the circle but not at the center. For these angles, the angle measure is one half the sum of the arc measures of the two subtended arcs.
- External angles: These are angles whose vertex is outside the circle. They can be secant-secant angles or secant-tangent angles. For these angles, the angle measure is one half the difference of the arc measures of the subtended arcs.