Nov 24

Free Body Diagrams when velocity is constant

By Tutor GuyNo Comments

 

Acceleration is the rate of change of the velocity. So if you are told that an object is stationary or is moving at constant velocity, this means the acceleration is zero. From Newton’s Second Law (F = ma), if the acceleration is zero, this means the net force is zero. So whenever velocity is constant, all the forces in the x and y directions must cancel out! Here’s a problem that shows how this concept is a powerful tool for solving free body problems:

Example: Jack pushes a large crate across a level surface at a constant speed. The crate has a mass of 50 kg and Jack exerts a horizontal force of 200 N. What is the coefficient of friction, μ?

 

 

 

 

 

 

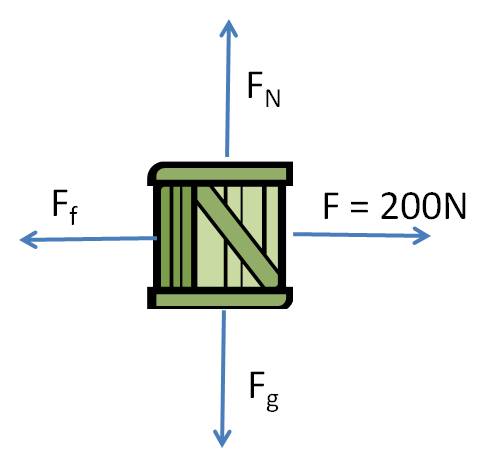
Answer: It seems that we don’t have enough information because we don’t know the velocity of the crate. But the fact that the speed is constant tells us that the net force is zero. So the solution is straightforward. First draw the free body diagram:

 

 

 

 

 

 

 

 

 

 

 

Because the net force is zero, the weight Fg is equal in magnitude to FN.

F_N=F_g=mg=(50)(9.8)=490 \, N

And because the net force is zero, the force Jack exerts is equal in magnitude to the frictional force.

F_f= \mu F_N=F \rightarrow \mu (490)=200 \rightarrow \mu = 0.41

Physics
,
Nov 21

Finding the angles of the gravity components in a ramp problem

By Tutor GuyNo Comments

 

In a ramp (or inclined plane) problem, the angle of the ramp is the same as the angle the gravity vector makes with the component normal to the ramp.

 

 

 

 

 

 

 

 

Here’s how you can be sure this is true: Look at the component of the gravity vector that is perpendicular to the ramp. Imagine that the ramp is horizontal—that is, θ is currently 0. Then the perpendicular component points straight down so that it coincides with Fg. Now start lifting the ramp. As the ramp angle increases, so does the angle between the perpendicular component and the gravity vector. You can see that these two angles have to be the same.

Physics
,
Nov 17

Units vs. Quantities in electromagnetism

By Tutor GuyNo Comments

 

Keeping the abbreviations straight in electromagnetism is particularly hard because sometimes the abbreviation we use for a QUANTITY is the same letter we use to define a UNIT of a different quantity. For example, a capital C is used for capacitance in the equation C = Q/V. But in the statement Q = 0.050 C, the C stands for ‘coulomb’, the unit of charge. It is up to you to understand from the context whether the symbol refers to a quantity or a unit.

Also, the symbol for a QUANTITY often comes from a German abbreviation, so it’s not the letter you expect. For example, the symbol for inductance is L, not I, and the symbol for current is I, not C. Again, it’s up to you to learn these well enough that you can figure them out on your own. Here’s a table that shows the various symbols:

Quantity

Symbol   for quantity

Unit

Symbol   for unit

force

F

newton

N

charge

Q

coulomb

C

electric field

E

N/C or V/m

current

I

ampere

A

potential difference

V

volt

V

resistance

R

ohm

Ω

power

P

watt

W

capacitance

C

farad

F

magnetic flux

Φ

weber

Wb

inductance

L

henry

H

magnetic field

B

tesla

T
Physics
, ,
Nov 14

Mastering units in electromagnetism

By Tutor GuyNo Comments

 

Almost all of the units we use in electromagnetism are named after dead physicists, so they can be difficult to remember and distinguish. Consider making a flash card with a list of all the quantities and units as a quick reference guide until you have them memorized.

Quantity

SI   Unit

Symbol

Equivalent   units

force

 newton

N

 kg·m/s2

charge

 coulomb

C

 A·s
current ampere

A

potential difference

 volt

V

resistance

 ohm

Ω

 V/A
power watt

W

V·A
capacitance farad

F

A·s/V

magnetic flux

 weber

Wb

V·s

inductance

 henry

H

V·s/A
magnetic field tesla

T

Wb/m2
Physics
, ,
Nov 10

Ideal Gas Law vs. Combined Gas Law

By Tutor GuyNo Comments

 

When you are doing gas law problems, your first decision should be whether to use the Ideal gas law or the combined gas law. How do you know which to use?

 

 

 

The Ideal Gas Law is used when you have one set of conditions for your system. Then if you know any three of the values for pressure, volume, moles and temperature, you can solve for the unknown quantity. The Combined Gas Law is used when you have two sets of conditions. In other words, you know the initial pressure, volume and temperature, and two of those quantities change to a new set of conditions. Then you can calculate the new value of the third quantity.

Example 1: What is the volume of a container that holds 0.561 mol of a gas at 1.15 atm at 27°C?

Answer: This problem describes a single set of conditions, so use the Ideal Gas Law:

PV=nRT

(1.15 \, atm)(V)=(0.561 \, mol) \! \left ( 0.0821 \, \frac{\ell \cdot atm}{mol \cdot K} \right ) \! (300 \, K)

V=12.0 \, L

Example 2: A 3.00 L container holds an ideal gas at STP. What will the new pressure be if the volume is increased to 3.75 L and the temperature is increased to 500 K?

Answer: This problem describes an initial condition and a new set of conditions, so use the combined gas law:

\dfrac{P_1V_1}{T_1}= \dfrac{P_2V_2}{T_2}

\dfrac{(1.00 \, atm)(3.00 \, L)}{273 \, K}= \dfrac{(P)(3.75 \, L)}{500 \, K}

P=1.47 \, atm

 

Chemistry
, ,
Nov 07

Average rate of change vs. instantaneous rate of change

By Tutor GuyNo Comments

 

The average rate of change on an interval is the slope of the secant line on that interval. The instantaneous rate of change at a point is the slope of the tangent line.

Example: In the picture below, the blue curve is f(x). The red segment is the secant line between x = 1 and x = 4. The slope of this line is the average rate of change between 1 and 4. The green line is the tangent line to the curve at x = 2. Its slope is the instantaneous rate of change of f(x) at x = 2.

 

 

 

 

 

 

 

 

 

 

 

 

 

To find the average rate of change between 1 and 4, determine the coordinates of the endpoints of the red secant line and calculate the slope. To find the instantaneous rate of change at x = 2, calculate f’(2).

Calculus
, , , ,
Nov 03

Confirming the Mean Value theorem

By Tutor GuyNo Comments

 

You are often asked to show an equation validates the Mean Value Theorem by finding the value of c that satisfies the conclusion of the theorem. The particular value of c you find does not matter in the slightest! All that’s important is that the value is in the interval between a and b.

Example: Find the value(s) of c that satisfies the conclusion of the Mean Value theorem for the function

f(x)= \dfrac{1}{x}

on the interval [½ ,6].

Solution: The function is continuous on the closed interval [1/2, 6] and differentiable on the open interval (1/2, 6), so the conditions of the Mean Value Theorem are met. Therefore, there must be a point c in the interval such that the derivative at that point is equal to the slope of the secant line between ½ and 6. The picture shows where that point is. (With a little practice, you can locate this point visually without much effort.)

 

 

 

 

 

 

 

 

 

As mentioned above, the particular value of c is not at all important. It is only important that we can locate it. We derive its value to show that it is indeed in the interval between ½ and 6.

First, find the slope of the secant line:

m=\dfrac{^1 \!\! / \!_6-2}{6- ^1 \!\! / \! _2}= \dfrac{^{-11} \!\! / \!_6}{^{11} \!\! / \! _2}= \dfrac{-1}{3}

Next, find a point c whose derivative is the same as the slope of the secant line:

f'(x)= \dfrac{-1}{x^2}= \dfrac{-1}{3} \rightarrow x= \pm \sqrt{3}

The positive value is in the interval, so the Mean Value Theorem has been demonstrated. (The negative value is not in the interval, but we do not care.)

Calculus
, , ,
Oct 31

Finding the equation of a tangent line to a curve

By Tutor GuyNo Comments

 

Finding the equation of a line that’s tangent to a function at a given point is not nearly as hard as it sounds. Think about what you need to write the equation of a line: a point and a slope. That’s all. Well, you’ve already been given the point. [If you don’t have the y-coordinate, just plug the x-coordinate into the function.] To find the slope, just take the derivative at the given value of x.

Example: Find the equation of the line tangent to the curve

when x = 4.

 

Solution: To find an equation for a line, you need a point and a slope. The tangent line touches the curve, so find the y-coordinate of the point on the curve when x = 4.

so the point is (4, 2). Now find the slope by finding the derivative at x = 4:

Now use the point-slope form to write the equation of the line:

Calculus
, , ,
Oct 27

Figuring out u substitutions

By Tutor GuyNo Comments

 

To determine if a ‘u substitution’ is appropriate for an integral, look for the value of du somewhere in the original integral. You may need to multiply or divide by a constant to get du in the integral.

Example 1: Integrate:

\displaystyle \int 3x^2e^{x^3} \, dx

Here the obvious choice for u \text{ is } x^3. And the derivative of x^3=3x^2, so du is in the integral too. Make the substitutions and solve:

\displaystyle \int 3x^2e^{x^3} \, dx = \int e^u \, du=e^u+C=e^{x^3}+C

Example 2: Integrate:

\displaystyle \int (x+1)(x^2+2x)^3 \, dx

 Do you see that x + 1 is the derivative of x^2+2x if we multiply x+1 by 2? Therefore, let u=x^2+2x, and du=2x+2=2(x+1) \, dx. To get the factor of 2 in the integral, multiply by 2 and multiply on the outside by ^1 \!\! / \! _{2.} The problem then becomes:

\displaystyle \int (x+1)(x^2+2x)^3 \, dx= \frac{1}{2} \int 2(x+1)(x^2+2x)^3 \, dx

\displaystyle = \frac{1}{2} \int (u)^3 \, du= \frac{1}{8} u^4+C= \frac{1}{8}(x^2+2x)^4+C

Example 3: Integrate:

\displaystyle \int \tan x \, dx

How is this a u substitution problem? First, rewrite \tan x:

\displaystyle \int \tan x \, dx= \int \frac{\sin x \, dx}{\cos x}

 Now do you see the u sub? Let u= \cos x \text{ and }du=- \sin x \, dx. Multiply inside and outside the integral by -1 so you can make the following substitution and solve:

\displaystyle \int \tan x \, dx= \int \frac{\sin x \, dx}{\cos x}=- \int \frac{- \sin x \, dx}{\cos x}=- \int \frac{du}{u}

=- \ln |u|+C=- \ln | \cos x|+C

What if you let u= \sin x in this example? Then du= \cos x \, dx. This seems like a reasonable substitution. However, this will put dx in the denominator. And that’s a definite no no! Any time you make a u substitution, the du term must be in the numerator.

Note: There are a couple of instances where a u substitution works and du isn’t in the original integral. You will learn these with a little practice. Here’s one example. Note that the radical term is not the derivative of the x term and the x term is not the derivative of the radical. However, with a little rearranging, a u substitution leads to an expression you can integrate:

\displaystyle \int x \sqrt{x+1} \, dx

\text{Let } u=x+1. \text{ Then } du=dx \text{ and } x=u-1. Substituting gives

\displaystyle \int (u-1) \sqrt{u} \, du= \int u^{3/2}-u^{1/2} \, du= \frac{2}{5}u^{5/2}- \frac{2}{3}u^{3/2}+C

= \dfrac {2}{5}(x+1)^{5/2}- \dfrac{2}{3}(x+1)^{3/2}+C

Calculus
, , , ,
Oct 24

Factoring the sum or difference of two cubes

By Tutor GuyNo Comments

 

The sum or difference of two cubes can always be factored as follows:

(x^3+y^3)=(x+y)(x^2-xy+y^2)

(x^3-y^3)=(x-y)(x^2+xy+y^2)

 These formulas are not too easy to figure out on your own, so your best approach is to memorize them. But how do you keep straight where the plus and minus signs go? Some students like to use the acronym “SOAP”, which stands for Same-Opposite-Always Positive. This means that the first sign is the same as the sign in the sum or difference of the cubes, the second sign is the opposite of this sign, and the third sign is always positive.

Algebra 2
, , ,
< OlderNewer >
Blue Taste Theme created by Jabox