Bay Area Tutoring

Integrals involving trig substitutions

By Tutor GuyNo Comments

When is it appropriate to solve an integral with a trig substitution? First of all, keep in mind that a trig substitution doesn’t always work. Even when it does work, you are often left with an integral that will require other techniques such as a u substitution or integration by parts. But if you are willing to put in a little effort (and you know your trig identities), trig substitutions allow you to find the antiderivatives of some rather complicated functions.

There are three conditions that you look for—each a radical term of a particular form in the integrand. Each condition is associated with a different substitution. After you make the substitution, you simplify the integrand and go from there.

Term	Substitution	Radical becomes…
$\sqrt{a^2-x^2}$	$\text{Let } x=a \sin \theta; \, dx=a \cos \theta \,d \theta$	$a \cos \theta$
$\sqrt{a^2+x^2}$	$\text{Let } x=a \tan \theta; \, dx=a \sec^2 \theta \,d \theta$	$a \sec \theta$
$\sqrt{x^2-a^2}$	$\text{Let } x=a \sec \theta; \, dx=a \sec \theta \tan \theta \,d \theta$	$a \tan \theta$

Before we look at some example integrals, let’s see why the first radical term above simplifies to $a \cos \theta.$ It’s pretty straightforward if you know your trig identities:

$\sqrt{a^2-x^2}=\sqrt{a^2-(a \sin \theta)^2}= \sqrt{a^2-a^2 \sin^2 \theta}= \sqrt{a^2(1- \sin^2 \theta)} =$

…….. $\sqrt{a^2 \cos^2 \theta} = a \cos \theta$

Example. Integrate the following:

$\text{a.} \displaystyle \int \frac{dx}{\sqrt{1-x^2}} \qquad \text{b.} \int \frac{x^3}{8 \sqrt{4+x^2}}dx \qquad \text{c.} \int x \sqrt{x^2-4} \; dx$

Solutions:

(Does this integral look familiar?) Here, $a=1$ , so use $x= \sin \theta.$ Using the first line of the table above:
…..
$\displaystyle \int \frac{dx}{\sqrt{1-x^2}}= \int \frac{\cos \theta \, d \theta}{\cos \theta}= \int d \theta = \theta +C$
…..
But since $x= \sin \theta, \theta=\sin^{-1} x.$
…..
$\therefore \displaystyle \int \frac{dx}{\sqrt{1-x^2}}=\sin^{-1} x+C$
Here, $a=2$ and we use line 2 from the table above $(x=2 \tan \theta).$ Note that $x^3=8 \tan^3 \theta.$ Upon substitution,
…..
$\displaystyle \int \frac{x^3}{8 \sqrt{4+x^2}}\, dx= \int \frac{8 \tan^3 \theta}{8(2 \sec \theta)}2 \sec^2 \theta \, d \theta = \int \tan^3 \theta \sec \theta \, d \theta$
…..
Hmm. This is going to take a little bit of extra work… Time to pull out some trig identities:
…..
$\int \tan^3 \theta \sec \theta \, d \theta = \int \tan^2 \theta \tan \theta \sec \theta \, d \theta = \int (\sec^2 \theta -1) \tan \theta \sec \theta \, d \theta$
…..
Now a u substitution, letting $u= \sec \theta$ :
…..
$\displaystyle \int (u^2-1) \, du= \frac{1}{3} u^3-u+C= \frac{1}{3} \sec^3 \theta - \sec \theta +C$
…..
How do we get our answer back in terms of $x?$ Draw a triangle that shows how $x$ and $\tan \theta$ are related, then use the Pythagorean theorem to find an expression for $\sec \theta.$ In the triangle below,
…..
$x=2 \tan \theta \therefore \sec \theta = \dfrac{\sqrt{4+x^2}}{2}$
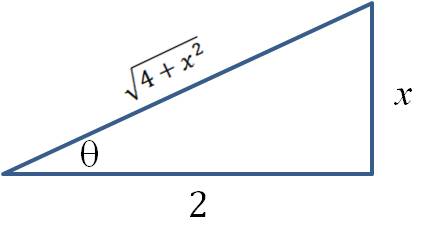Substitute into the integral above to get:
$\displaystyle \int \frac{x^3}{8 \sqrt{4+x^2}} dx=\frac{1}{3} \sec^3 \theta - \sec \theta +C= \frac{(4+x^2)^{3/2}}{24}- \frac{(4+x^2)^{1/2}}{2}+C$

This can be simplified further by factoring:
…..
$\displaystyle \int \frac{x^3}{8 \sqrt{4+x^2}}dx= \frac{(4+x^2)^{3/2}}{24}- \frac{(4+x^2)^{1/2}}{2}+C= \frac{1}{24}(x^2-8) \sqrt{4+x^2}$
…..
Whew!
This is a trick question. Even though it fits the condition given in the table (and you could integrate with a trig substitution if you wanted), it’s easier to do this one with a u substitution: $u=x^2-4$ and $du=2x \; dx:$
…..
$\displaystyle \int x \sqrt{x^2-4} \, dx= \frac{1}{2} \int \sqrt{u} \, du= \frac{1}{3}u^{3/2}+C= \frac{1}{3}(x^2-4)^{3/2}+C$

The lesson here is to look for u substitutions before you look for trig substitutions.

Feb 23

u substitutions with definite integrals

By Tutor GuyNo Comments

When a definite integral requires a u substitution to solve, be sure to substitute for the limits of integration as well. This way, you don’t need to substitute back in for the original function. Instead, you evaluate the integral using the new (u) limits. Here’s an example to show how this works.

Evaluate:

$\displaystyle \int_0^{\pi/4} \sec^2 \theta \tan^2 \theta \; d \theta$

This is an obvious candidate for a u substitution. (See other posts on this website for more information on when to use u substitutions.)

Let $u= \tan \theta$ . Then $du=\sec^2 \theta \; d \theta$ .

But don’t stop there! Use your expression for u to determine the new limits as well.

$\theta =0 \rightarrow u=0; \; \theta= \dfrac{\pi}{4} \rightarrow u=1$

So the new integral becomes

$\displaystyle \int_0^{\pi/4} \sec^2 \theta \tan^2 \theta \; d \theta =\int_0^1 u^2 \; du= \left. \dfrac{1}{3}u^3 \right |_0^1=\dfrac{1}{3}-0=\dfrac{1}{3}$

You have found the solution to the original integral without needing to put the integral back in terms of $\theta$ .

Jan 05

Strategies for finding integrals

By Tutor GuyNo Comments

How does one become an “expert integrator”? There are a lot of integration techniques, and recognizing which technique is the best is the first step to finding the integral. Many new calculus students look at an integral and don’t even know where to start. Here is a strategy you can adopt when faced with an integral. Carry on this internal dialog with yourself:

Is this something that I can integrate by inspection?
Is this an integral that can be turned into an elementary integral by simplifying?
Is there a trig identity that will simplify the integral?
Is it a candidate for a u substitution?
Can I use integration by parts?
Will decomposition by partial fractions be useful?
Does the integral involve a product of trig functions?
Would a trig substitution be effective?
Can I find it in a table of integrals?

Yes, this is a long list. But with practice, you can work your way through it pretty quickly. [If you are taking Calc AB this year, you will only learn the first four or five steps.] Think of each integration technique as a tool for your toolbox; with each integral you encounter, you decide which tool is the best for that problem.

Let’s look at a couple of examples to see how this works.

Example 1. Evaluate:

$\displaystyle \int {\sec}^2 x+x^2-2x \; dx$

This is an integral consisting of only elementary derivatives, so you can integrate it by inspection:

$\displaystyle \int {\sec}^2 x+x^2-2x \; dx = \tan x+ \dfrac{1}{3}x^3-x^2+C$

Note that you need to know the derivatives of the elementary functions in order to recognize when you can integrate by inspection. This means the derivatives of the trig functions, exponential and log functions and the inverse trig functions, not just polynomials.

Example 2. Evaluate:

$\displaystyle \int (x^2-1)(2x^2+3x) \; dx$

This is not an elementary derivative, so it cannot be integrated by inspection. But the integrand can by simplified by multiplying the terms out, turning it into an elementary derivative:

$\displaystyle \int (x^2-1)(2x^2+3x) \; dx \displaystyle \int 2x^4+3x^3-2x^2-3x \; dx=\dfrac{2}{5}x^5+\dfrac{3}{4}x^4-\dfrac{2}{3}x^3- \dfrac{3}{2}x^2+C$

Example 3. Evaluate:

$\displaystyle \int \tan^2 x \; dx$

This is not an elementary derivative. Is there a trig identity that will help? Yes, use the following Pythagorean identity to turn this into a simple integral:

$\displaystyle \int \tan^2 x \; dx = \displaystyle \int \sec^2 x-1 \; dx = \tan x-x+C$

At this point, you might be thinking “how am I supposed to see that identity?” Well, there’s no substitute for experience and practice. It’s important to know your basic trig identities, so you can rewrite a trig integral in a different form. If one identity doesn’t work, try another. Finding integrals is as much an art as it is a science. Be creative and be inventive.

(Look for other tips on integral problems on this website for strategies on u substitution, integration by parts, products of trig functions and trig substitutions.)

Oct 27

Figuring out u substitutions

By Tutor GuyNo Comments

To determine if a ‘u substitution’ is appropriate for an integral, look for the value of du somewhere in the original integral. You may need to multiply or divide by a constant to get du in the integral.

Example 1: Integrate:

$\displaystyle \int 3x^2e^{x^3} \, dx$

Here the obvious choice for $u \text{ is } x^3$ . And the derivative of $x^3=3x^2,$ so $du$ is in the integral too. Make the substitutions and solve:

$\displaystyle \int 3x^2e^{x^3} \, dx = \int e^u \, du=e^u+C=e^{x^3}+C$

Example 2: Integrate:

$\displaystyle \int (x+1)(x^2+2x)^3 \, dx$

Do you see that $x + 1$ is the derivative of $x^2+2x$ if we multiply $x+1$ by $2?$ Therefore, let $u=x^2+2x,$ and $du=2x+2=2(x+1) \, dx.$ To get the factor of $2$ in the integral, multiply by $2$ and multiply on the outside by $^1 \!\! / \! _{2.}$ The problem then becomes:

$\displaystyle \int (x+1)(x^2+2x)^3 \, dx= \frac{1}{2} \int 2(x+1)(x^2+2x)^3 \, dx$

$\displaystyle = \frac{1}{2} \int (u)^3 \, du= \frac{1}{8} u^4+C= \frac{1}{8}(x^2+2x)^4+C$

Example 3: Integrate:

$\displaystyle \int \tan x \, dx$

How is this a u substitution problem? First, rewrite $\tan x:$

$\displaystyle \int \tan x \, dx= \int \frac{\sin x \, dx}{\cos x}$

Now do you see the u sub? Let $u= \cos x \text{ and }du=- \sin x \, dx.$ Multiply inside and outside the integral by $-1$ so you can make the following substitution and solve:

$\displaystyle \int \tan x \, dx= \int \frac{\sin x \, dx}{\cos x}=- \int \frac{- \sin x \, dx}{\cos x}=- \int \frac{du}{u}$

$=- \ln |u|+C=- \ln | \cos x|+C$

What if you let $u= \sin x$ in this example? Then $du= \cos x \, dx.$ This seems like a reasonable substitution. However, this will put $dx$ in the denominator. And that’s a definite no no! Any time you make a u substitution, the $du$ term must be in the numerator.

Note: There are a couple of instances where a u substitution works and du isn’t in the original integral. You will learn these with a little practice. Here’s one example. Note that the radical term is not the derivative of the x term and the x term is not the derivative of the radical. However, with a little rearranging, a u substitution leads to an expression you can integrate:

$\displaystyle \int x \sqrt{x+1} \, dx$

$\text{Let } u=x+1. \text{ Then } du=dx \text{ and } x=u-1.$ Substituting gives

$\displaystyle \int (u-1) \sqrt{u} \, du= \int u^{3/2}-u^{1/2} \, du= \frac{2}{5}u^{5/2}- \frac{2}{3}u^{3/2}+C$

$= \dfrac {2}{5}(x+1)^{5/2}- \dfrac{2}{3}(x+1)^{3/2}+C$

Archive

Integrals involving trig substitutions

u substitutions with definite integrals

Strategies for finding integrals

Figuring out u substitutions

Tutor Guy Homework Tips