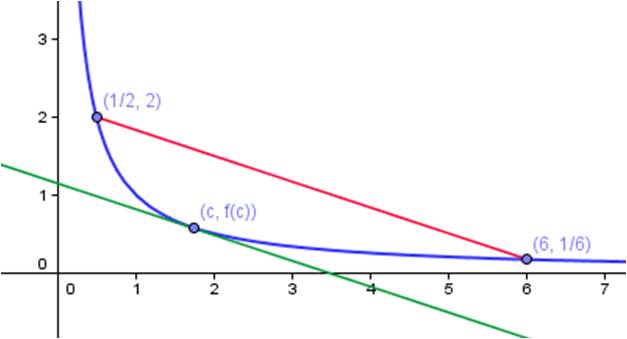
You are often asked to show an equation validates the Mean Value Theorem by finding the value of c that satisfies the conclusion of the theorem. The particular value of c you find does not matter in the slightest! All that’s important is that the value is in the interval between a and b.
Example: Find the value(s) of c that satisfies the conclusion of the Mean Value theorem for the function
on the interval [½ ,6].
Solution: The function is continuous on the closed interval [1/2, 6] and differentiable on the open interval (1/2, 6), so the conditions of the Mean Value Theorem are met. Therefore, there must be a point c in the interval such that the derivative at that point is equal to the slope of the secant line between ½ and 6. The picture shows where that point is. (With a little practice, you can locate this point visually without much effort.)
As mentioned above, the particular value of c is not at all important. It is only important that we can locate it. We derive its value to show that it is indeed in the interval between ½ and 6.
First, find the slope of the secant line:
Next, find a point c whose derivative is the same as the slope of the secant line:
The positive value is in the interval, so the Mean Value Theorem has been demonstrated. (The negative value is not in the interval, but we do not care.)