Often, a related rate problem will require a value for a variable, but you don’t have the value. When this occurs, use the original equation (before you took the derivative) to find the unknown value.
Example: Two cars leave an intersection at the same time. Car A travels north at 60 feet per second. Car B travels east at 80 feet per second. How fast is the distance between them changing 1.0 minute after the cars leave the intersection?
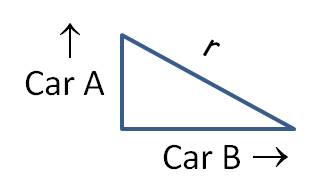
Solution: First draw a picture.
It makes sense to let y be the distance car A has traveled from the intersection, and let x be the distance car B has traveled from the intersection. There are two rates given in the problem, and we need to find a third rate:
It should be obvious from the picture that the Pythagorean Theorem provides the equation we need:
Differentiating gives:
To solve for dr/dt, we need to know the value of x, y and r. We can calculate x and y because the cars have been traveling for 60 seconds: x = 4800 ft and y = 3600 ft. To find r, we need to plug these values back into our original equation:
Then plug everything in to solve:
(Look for other tips on solving related rate problems on this website if you need help with other aspects of related rate problems.)