Archive

Jan 02

Related Rates: Substituting for extra variables

By Tutor GuyNo Comments

 

The most complicated type of related rate problems for many students is when there is a variable and you have no information about its rate of change. In these problems, you will know how the variable is related to another variable with a known rate. You can then substitute the variable with the known rate in for the variable with the unknown rate. It sounds difficult, but with a little practice, you can master it.

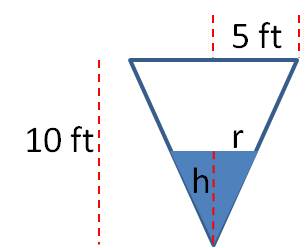
Example: A water tower in the shape of an inverted cone is being filled at a rate of 2 cubic feet per minute. The tower is 10 feet tall and the radius of the base is 5 feet. How fast is the depth of the water changing when the depth is 4 feet?

Solution: First, we draw a picture. This drawing shows a cross section of the water tower, filled to a height of h.

                       

 

 

 

 

 

 

 

 

The variables we know and seek are the following:

\dfrac{dV}{dt}=2; \; \dfrac{dh}{dt}= \, ?

The variables suggest that the equation we need is the volume of a cone:

V= \dfrac{1}{3} \pi r^2h

If we take the derivative now, we will end up with a dr/dt term but we are not given any information about how fast the radius is changing. We get around this problem by solving for r in terms of h and substituting. How are r and h related? Notice that the triangle of water in the drawing above is similar to the triangle of the whole water tower. This means we can set up the following relationship:

\dfrac{5}{10}= \dfrac{r}{h} \rightarrow r= \dfrac{h}{2}

No matter how deep the water is at any time, the radius of the water surface will always be half the height of the water column. Substituting into our equation and simplifying:

V= \dfrac{1}{3} \pi r^2h \rightarrow V= \dfrac{1}{3} \pi \left ( \dfrac{h}{2} \right )^2h \rightarrow V= \dfrac{1}{12} \pi h^3

Now that r has been eliminated, we can differentiate:

\dfrac{dV}{dt}=\dfrac{\pi}{4}h^2 \dfrac{dh}{dt}

Plugging in values gives:

2= \dfrac{\pi}{4}(4)^2 \dfrac{dh}{dt}, \qquad \text{so } \dfrac{dh}{dt}= \dfrac{1}{2 \pi} \, ft/min

(Look for other tips on solving related rate problems on this website if you need help with other aspects of related rate problems.)

Dec 29

Related Rates: Finding missing variables

By Tutor GuyNo Comments

 

Often, a related rate problem will require a value for a variable, but you don’t have the value. When this occurs, use the original equation (before you took the derivative) to find the unknown value.

Example: Two cars leave an intersection at the same time. Car A travels north at 60 feet per second. Car B travels east at 80 feet per second. How fast is the distance between them changing 1.0 minute after the cars leave the intersection?

Solution: First draw a picture.

 

 

 

 

 

 

It makes sense to let y be the distance car A has traveled from the intersection, and let x be the distance car B has traveled from the intersection. There are two rates given in the problem, and we need to find a third rate:

\dfrac{dy}{dt}=60; \; \dfrac{dx}{dt}=80; \; \dfrac{dr}{dt}= \, ?

 It should be obvious from the picture that the Pythagorean Theorem provides the equation we need:

x^2+y^2=r^2

 Differentiating gives:

2x \dfrac{dx}{dt}+2y \dfrac{dy}{dt}=2r \dfrac{dr}{dt} \rightarrow x \dfrac{dx}{dt}+y \dfrac{dy}{dt}=r \dfrac{dr}{dt}

 To solve for dr/dt, we need to know the value of x, y and r. We can calculate x and y because the cars have been traveling for 60 seconds: x = 4800 ft and y = 3600 ft. To find r, we need to plug these values back into our original equation:

x^2+y^2=r^2 \rightarrow (4800)^2+(3600)^2=r^2 \rightarrow r=6000

Then plug everything in to solve:

x \dfrac{dx}{dt}+y \dfrac{dy}{dt}=r \dfrac{dr}{dt} \rightarrow (4800)(80)+(3600)(60)=(6000) \dfrac{dr}{dt} \rightarrow \dfrac{dr}{dt}=100 \, ft/s

(Look for other tips on solving related rate problems on this website if you need help with other aspects of related rate problems.)

Dec 26

Related Rates: Defining Variables

By Tutor GuyNo Comments

 

Related rate problems will no longer seem so complicated once you master the art of defining rates as variables. And not just any variables, but variables in the form of derivatives! In other words, express the known and unknown rates as derivatives such as dV/dt or dA/dt. Remember that dA/dt means “the rate of change of the Area”. Your task is to find expressions for rates in the problem and “translate” them from English into Calculus. Here are some examples:

  • “The radius is increasing at a rate of 3.0 cm/s.”

\dfrac{dr}{dt}=3.0

  •  “If the volume is decreasing at a rate of 1.5 liters per minute…”

\dfrac{dV}{dt}=-1.5

  • “How fast is the ladder falling down the side of the building?”

\dfrac{dy}{dt}= \, ?

 Remember that speed at which something moves is the rate of change of its position. Also, this derivative expresses the unknown we are going to find in the problem.

  • “The temperature is dropping by 2.3° per hour.”

\dfrac{dT}{dt}=-2.3

 Note that when a value is falling or decreasing, the value of the derivative is negative.

Once you have defined all your rates as variables, your next step is to write the equation that expresses one variable in terms of the others. However, the equation has to be in terms of the quantities in the numerators, not in terms of the derivatives. Yes, this seems all wrong, but you will get the derivatives when you differentiate each side of the equation. For example, if your two rates are dV/dt and dr/dt, then you need to write an equation that expresses V in terms of r. When you differentiate this equation, you get the related rates equation and can plug in all the values you have.

Example: A hot air balloon in the shape of a sphere is being filled with gas at the rate of 20 cubic meters per minute. How fast is the radius changing when the volume is 288π cubic meters?

Solution: First, find all the rates mentioned in the problem:

\dfrac{dV}{dt}=20; \; \dfrac{dr}{dt}= \, ?

 Now, you need an equation that relates volume (V) to radius (r). Because the balloon is a sphere, use the formula for the volume of a sphere:

V= \dfrac{4}{3} \pi r^3

 Next, differentiate with respect to time:

\dfrac{dV}{dt}=4 \pi r^2 \dfrac{dr}{dt}

 This equation includes r. You need to plug in the value of V in the original equation to solve for r:

V= \dfrac{4}{3} \pi r^3 \rightarrow 288 \pi= \dfrac{4}{3} \pi r^3 \rightarrow 216=r^3 \rightarrow r=6 \, m

 Now plug in all the values to solve for the unknown rate:

\dfrac{dV}{dt}=4 \pi r^2 \dfrac{dr}{dt} \rightarrow 20=4 \pi (6)^2 \dfrac{dr}{dt} \rightarrow \dfrac{dr}{dt}= \dfrac{20}{4 \pi (36)} \approx 0.044 \, m/min

 (Look for other tips on solving related rate problems on this website if you need help with other aspects of related rate problems.)

Dec 22

Related Rates: Getting Started

By Tutor GuyNo Comments

 

The most valuable first step when doing a related rate problem is to draw a picture. This helps you figure out the geometry of the problem.

Example: A boat is being towed to a dock by a rope attached to a winch that is five feet higher than the boat. If the winch is pulling the rope at 1.2 m/s, how fast is the boat moving when it is 12 m from the dock?

Solution: It would be very difficult to set up and solve this problem without a quick sketch. But once you draw the picture (and label the components as shown), you can see that a simple right triangle describes the situation.

 

 

 

 

 

The equation you need is therefore:

Differentiating gives:

So the boat is approaching the dock at 1.3 m/s.

(Look for other tips on solving related rate problems if you need help with some of the details of the solution.)

Blue Taste Theme created by Jabox