What’s the easiest way to find the inverse of a 3×3 matrix? Use your graphing calculator, of course! But if you need to find the inverse without a calculator, here’s a method that will give you the solution with the least amount of trouble. We’ll demonstrate with an example.
Find the inverse of the following matrix:
The first step in finding the inverse is to calculate the determinant of the matrix. The easiest way to calculate a 3×3 determinant is to write the matrix out, and append the first two columns at the end:
From here, you need to find the six different products along each of the diagonals shown:
Add the blue products together and add the red products together, then subtract the red total from the blue total: . This is the determinant. By the way, if the determinant is
, stop. Your matrix does not have an inverse.
Next, you need to find the elements of the inverse matrix. Here’s a clever trick that will help you do that. Start by writing the transpose of the original matrix. This is done by changing all the rows into columns:
Then write the first two columns over on the right and the first two rows over again on the bottom. Your array should look like this:
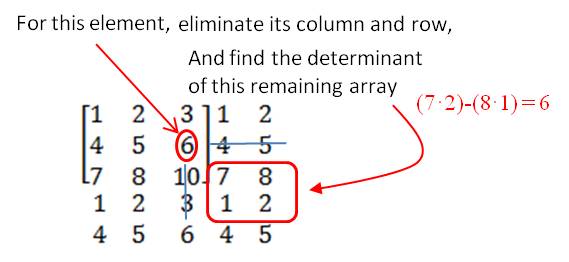
The next step is a little tricky to explain, though once you’ve done it, it’s pretty easy to figure out. For each of the nine positions in the matrix, you find the value of the determinant of the 2×2 array that is just below it and to the right. [One way to think of this is that each position in the matrix is the upper-left number of a 3×3 array. If you mentally delete the first row and column of that array, you have a 2×2 array left. This is the array for which you find a determinant. I demonstrate this below with the and the
from the array above.
Do this process for all nine elements of the matrix and you should end up with this matrix:
Finally, divide this matrix by the determinant you found above. The result will be the inverse of the original matrix:
I’ll leave it to you to verify that this is indeed the inverse of the original matrix. For any 3×3 matrix that has an inverse, this method will calculate it for you correctly every time.