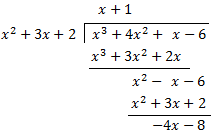Bay Area Tutoring

 

In a previous post, I listed the steps you need to follow to analyze and graph a rational function. In this post, I show you how to find the horizontal or oblique asymptotes, if they exist. If there are no horizontal or oblique asymptotes, then you can determine the end behavior of the function. [Check other posts on this website for other steps in analyzing and graphing a rational function.]

The horizontal and oblique asymptotes, if they exist, tell you the end behavior of the function. That is, they describe what the function is doing as goes to ±∞. In order to determine the end behavior, examine the degrees of the polynomials in the numerator and denominator. There are four possible cases:

Case 1: The degree of the denominator is greater than the degree of the numerator.

When the denominator has the higher degree, the denominator grows much faster than the numerator as gets very large. Like all fractions, as the denominator gets very large, the fraction gets very small and approaches zero. So the asymptote is .

Example 1: Find the end behavior for the following rational function:

Solution: Because the degree of the numerator is and the degree of the denominator is , this function has a horizontal asymptote .

Case 2: The degree of the denominator is equal to the degree of the numerator.

When the degrees of the numerator and denominator are the same, the function approaches a finite non-zero number. This number is the ratio of the leading coefficients of the two polynomials and this is the value of the horizontal asymptote.

Example 2: Find the end behavior for the following rational function:

 Solution: Because the degree of the numerator and denominator are the same, this function has a horizontal asymptote. Divide the leading coefficients ( and ) and the horizontal asymptote is .

 

Case 3: The degree of the numerator is exactly one higher than the degree of the denominator.

In this case, there is an oblique asymptote (called a slant asymptote in some textbooks). To find the asymptote, divide the denominator into the numerator using long division. The quotient is the oblique asymptote. (Ignore the remainder; it has no effect on the asymptote.)

Example 3: Find the end behavior for the following rational function:

 Here, the numerator (degree 3) is exactly one higher than the denominator (degree 2). To find the asymptote, perform the following long division:

 

 

 

 

 

The quotient is the oblique asymptote:

Case 4: The degree of the numerator is more than one higher than the degree of the denominator.

In this case, there is no horizontal or oblique asymptote. Instead, the end behavior of the function is the same as the end behavior of a polynomial whose degree is the same as the difference between the degrees of the numerator and the denominator. For example, if the numerator is degree and the denominator is degree , the rational function will look like a cubic function as approaches ±∞.