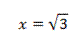Optimization problems can be tamed if you remember one simple idea. The purpose of an optimization problem is to optimize the situation. That is, you want to find where the results are the biggest, or the smallest, or the fastest, or the highest. In other words, if you can find an equation that describes the situation, you are being asked to find the relative minimum or relative maximum of that function. So break these problems down into three steps:
- Determine what parameter you are optimizing.
- Write a formula that gives that parameter in terms of an independent variable.
- Take the derivative to find the relative min and/or max.
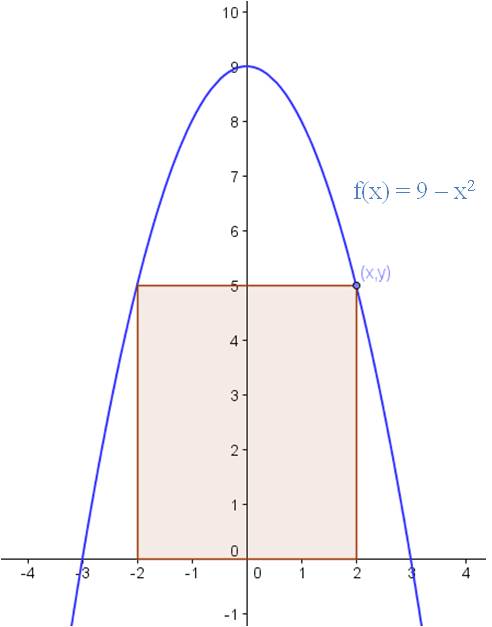
Example: What are the dimensions of the rectangle with the largest area that can be inscribed above the x-axis and under the function f(x) = 9 – x2?
Solution: (Step 1) In this case, you are trying to maximize area. So you need (Step 2) a formula that gives the area in terms of the x-variable. Let’s draw a picture:
We can see from the sketch that if the upper right corner of the rectangle is on the point (x,y), the base of the rectangle is 2x and the height is y. So our first effort at an equation for the area is
A = 2xy.
To finish the problem, we need to express y in terms of x. Since the point is on the parabola, y = 9 – x2. Therefore, the equation we seek is
A = 2x(9 – x2) = 18x – 2x3.
To find the dimensions of the largest possible area, we find the relative maximum of the equation (Step 3).
A’ = 18 – 6x2 = 0 → x2 = 3
Plugging back into the equation for y gives y = 6.