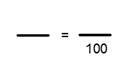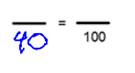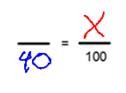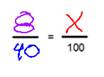Aug 11

Triangle Congruence Proofs and CPCTC

By Tutor GuyNo Comments

 

The triangle congruence theorems (SSS, SAS, ASA and HL) can only be used to show that two triangles are congruent to each other. You can’t use them to show that sides or angles are congruent.

However, CPCTC is used to show that parts of triangles are congruent to each other. CPCTC cannot be used to show that triangles are congruent.

When you construct a proof that asks you to show that two segments or two angles in a triangle are congruent, most of the time you will first show the triangles are congruent, and then use CPCTC to show the corresponding parts are congruent.

Remember that CPCTC can’t be used until you have already shown that the triangles are congruent.

Geometry
, , ,
Aug 08

The zero property

By Tutor GuyNo Comments

Perhaps the most important property you’ll learn in Algebra 1 is the zero property.

It says that if a · b = 0, then either a = 0 or b = 0 (or both).

This property allows us to solve most of the equations we encounter in algebra and beyond. First, move everything to one side of the equation (so the other side equals 0). Second, factor the equation. Then we can set each factor equal to zero and solve.

You will use this technique (on more and more complicated equations) in every math class you take.

Example: Solve x2 = 3x.

Solution:

 

x2 – 3x = 0

 (Move everything to one side.)

x(x-3) = 0

 (Factor.)

x = 0 or x-3 = 0

 (Set each factor equal to 0.)

x = 0 or x = 3

 (Solve each factor.)
Algebra 1
, ,
Aug 05

Solving for x

By Tutor GuyNo Comments

 

“Solve for x” simply means “Get x all by itself on one side of the equation”.  Of course, when x is by itself, it must be equal to whatever is on the other side of the equals sign.

What makes this so important? Sometimes we are interested in solving for other quantities besides x, and if we can isolate that value, the solution can be easy to find.

Example: Solve for x^2+y^2

\begin{array}{rl} x^2z^2+y^2z^2-w^2 & =0 \\ x^2z^2+y^2z^2 & =w^2 \\ z^2(x^2+y^2) & =w^2 \\ x^2+y^2 & =\dfrac{w^2}{z^2} \end{array}

Algebra 1
, , ,
Aug 01

Solving percentage problems

By Tutor GuyNo Comments

 

Percentage problems such as “8 is what percent of 40?” will be a snap for you if you remember this simple procedure.  The trick is to set the problem up as a simple proportion—in other words, you make two fractions equal to each other. Then all you have to do is place all the numbers in the correct positions by following the rules below. Let’s see how to solve the problem above.

  • First, write two fractions, but put only the 100 on the bottom of the right fraction:

 

 

  • Now, look at the problem and find the number right after the word “of”. In this case, it’s 40. Place that number on the bottom of the left fraction:

 

 

  • Next, find the number right before the word “percent”. This number goes over the 100. In this problem, there is no number before “percent”; it’s the word ‘what’. When you see ‘what’, that’s your variable! Place an x over the 100.

 

 

 

  • The last number goes on the top of the left fraction. In this problem, that’s 8.

 

 

  • Once you’ve filled in all the spaces, you solve the usual way, by cross-multiplying:
    40x = 800
    x = 20.      So 8 is 20% of 40.

We can summarize by describing a general percentage problem: A is B percent of C?
Here, A, B and C represent numbers or the word ‘what’ (in which case it is the variable). C (the number following ‘of’) goes on the bottom next to the 100. B (the number before ‘percent’) goes above the 100, and A (the remaining number) goes in the last space. Then cross multiply and solve.

Algebra 1
, ,
Newer >
Blue Taste Theme created by Jabox