A good strategy for completing a proof in geometry is to work backwards. If you are having trouble determining where to start, try going to the end first. Look at the statement you are trying to prove and ask yourself, “What do I need to know in order to prove this statement?” In other words, what would the last line of the proof be? Then figure out what you need in order to prove the next to last line of the proof, and so on.
Here’s an example to show how this works:
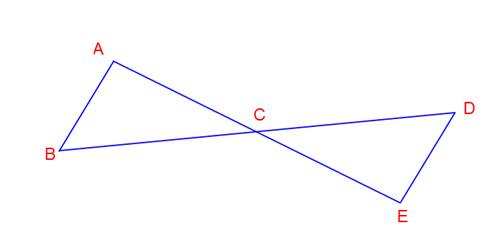
Given: and
bisect each other.
Prove:
How do you approach this? The first question to ask yourself is “what do I need to know to prove the two segments are congruent?” The answer: Show that the two triangles are congruent—then the segments will be congruent by CPCTC.
So next, the question becomes “how do I show that the triangles are congruent?” Well, you can show triangles are congruent with SSS, SAS or ASA.
Continuing to work backwards, the next question is “can I prove SSS?” Well, no, because you’re trying to prove two sides are congruent. You can’t use what you’re trying to prove in a congruence proof! So ask the next question: “can I prove SAS?” And the answer is yes!
Because and
bisect each other,
and
And
because they are vertical angles.
You have simplified the proof to finding two congruent sides and a congruent angle. This leads to SAS which leads to two congruent triangles which leads to the two congruent segments you were trying to prove.