Archive

For the Calculus category

Nov 07

Average rate of change vs. instantaneous rate of change

By Tutor GuyNo Comments

 

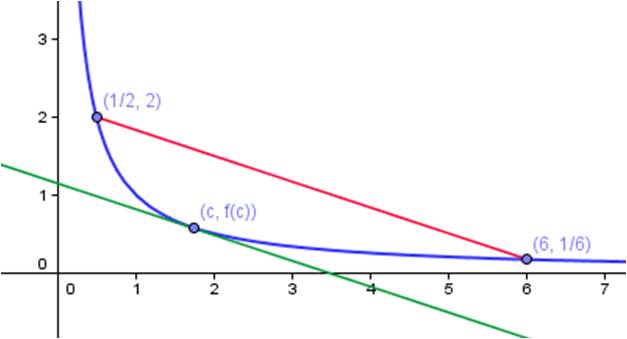
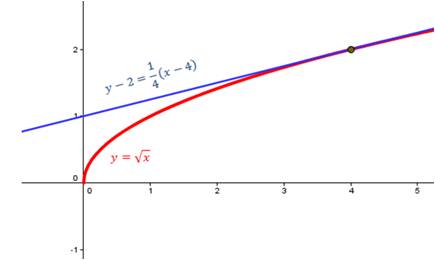
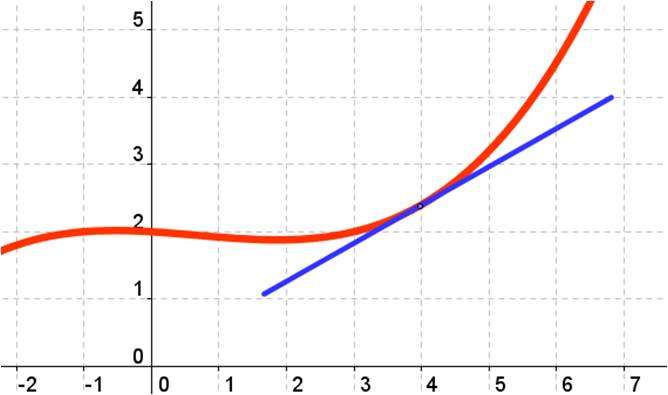
The average rate of change on an interval is the slope of the secant line on that interval. The instantaneous rate of change at a point is the slope of the tangent line.

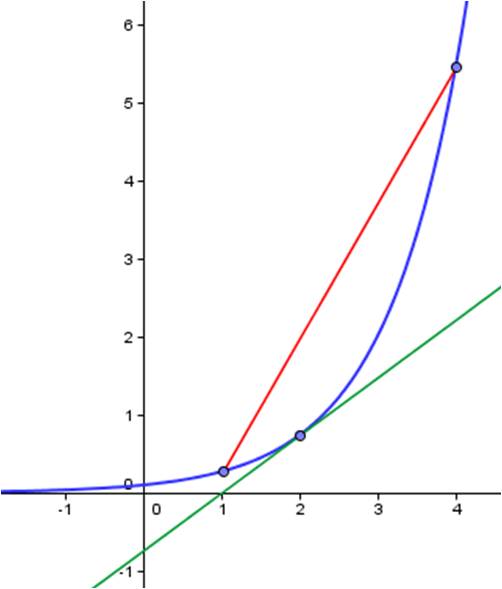
Example: In the picture below, the blue curve is f(x). The red segment is the secant line between x = 1 and x = 4. The slope of this line is the average rate of change between 1 and 4. The green line is the tangent line to the curve at x = 2. Its slope is the instantaneous rate of change of f(x) at x = 2.

 

 

 

 

 

 

 

 

 

 

 

 

 

To find the average rate of change between 1 and 4, determine the coordinates of the endpoints of the red secant line and calculate the slope. To find the instantaneous rate of change at x = 2, calculate f’(2).

Nov 03

Confirming the Mean Value theorem

By Tutor GuyNo Comments

 

You are often asked to show an equation validates the Mean Value Theorem by finding the value of c that satisfies the conclusion of the theorem. The particular value of c you find does not matter in the slightest! All that’s important is that the value is in the interval between a and b.

Example: Find the value(s) of c that satisfies the conclusion of the Mean Value theorem for the function

f(x)= \dfrac{1}{x}

on the interval [½ ,6].

Solution: The function is continuous on the closed interval [1/2, 6] and differentiable on the open interval (1/2, 6), so the conditions of the Mean Value Theorem are met. Therefore, there must be a point c in the interval such that the derivative at that point is equal to the slope of the secant line between ½ and 6. The picture shows where that point is. (With a little practice, you can locate this point visually without much effort.)

 

 

 

 

 

 

 

 

 

As mentioned above, the particular value of c is not at all important. It is only important that we can locate it. We derive its value to show that it is indeed in the interval between ½ and 6.

First, find the slope of the secant line:

m=\dfrac{^1 \!\! / \!_6-2}{6- ^1 \!\! / \! _2}= \dfrac{^{-11} \!\! / \!_6}{^{11} \!\! / \! _2}= \dfrac{-1}{3}

Next, find a point c whose derivative is the same as the slope of the secant line:

f'(x)= \dfrac{-1}{x^2}= \dfrac{-1}{3} \rightarrow x= \pm \sqrt{3}

The positive value is in the interval, so the Mean Value Theorem has been demonstrated. (The negative value is not in the interval, but we do not care.)

Oct 31

Finding the equation of a tangent line to a curve

By Tutor GuyNo Comments

 

Finding the equation of a line that’s tangent to a function at a given point is not nearly as hard as it sounds. Think about what you need to write the equation of a line: a point and a slope. That’s all. Well, you’ve already been given the point. [If you don’t have the y-coordinate, just plug the x-coordinate into the function.] To find the slope, just take the derivative at the given value of x.

Example: Find the equation of the line tangent to the curve

when x = 4.

 

Solution: To find an equation for a line, you need a point and a slope. The tangent line touches the curve, so find the y-coordinate of the point on the curve when x = 4.

so the point is (4, 2). Now find the slope by finding the derivative at x = 4:

Now use the point-slope form to write the equation of the line:

Oct 27

Figuring out u substitutions

By Tutor GuyNo Comments

 

To determine if a ‘u substitution’ is appropriate for an integral, look for the value of du somewhere in the original integral. You may need to multiply or divide by a constant to get du in the integral.

Example 1: Integrate:

\displaystyle \int 3x^2e^{x^3} \, dx

Here the obvious choice for u \text{ is } x^3. And the derivative of x^3=3x^2, so du is in the integral too. Make the substitutions and solve:

\displaystyle \int 3x^2e^{x^3} \, dx = \int e^u \, du=e^u+C=e^{x^3}+C

Example 2: Integrate:

\displaystyle \int (x+1)(x^2+2x)^3 \, dx

 Do you see that x + 1 is the derivative of x^2+2x if we multiply x+1 by 2? Therefore, let u=x^2+2x, and du=2x+2=2(x+1) \, dx. To get the factor of 2 in the integral, multiply by 2 and multiply on the outside by ^1 \!\! / \! _{2.} The problem then becomes:

\displaystyle \int (x+1)(x^2+2x)^3 \, dx= \frac{1}{2} \int 2(x+1)(x^2+2x)^3 \, dx

\displaystyle = \frac{1}{2} \int (u)^3 \, du= \frac{1}{8} u^4+C= \frac{1}{8}(x^2+2x)^4+C

Example 3: Integrate:

\displaystyle \int \tan x \, dx

How is this a u substitution problem? First, rewrite \tan x:

\displaystyle \int \tan x \, dx= \int \frac{\sin x \, dx}{\cos x}

 Now do you see the u sub? Let u= \cos x \text{ and }du=- \sin x \, dx. Multiply inside and outside the integral by -1 so you can make the following substitution and solve:

\displaystyle \int \tan x \, dx= \int \frac{\sin x \, dx}{\cos x}=- \int \frac{- \sin x \, dx}{\cos x}=- \int \frac{du}{u}

=- \ln |u|+C=- \ln | \cos x|+C

What if you let u= \sin x in this example? Then du= \cos x \, dx. This seems like a reasonable substitution. However, this will put dx in the denominator. And that’s a definite no no! Any time you make a u substitution, the du term must be in the numerator.

Note: There are a couple of instances where a u substitution works and du isn’t in the original integral. You will learn these with a little practice. Here’s one example. Note that the radical term is not the derivative of the x term and the x term is not the derivative of the radical. However, with a little rearranging, a u substitution leads to an expression you can integrate:

\displaystyle \int x \sqrt{x+1} \, dx

\text{Let } u=x+1. \text{ Then } du=dx \text{ and } x=u-1. Substituting gives

\displaystyle \int (u-1) \sqrt{u} \, du= \int u^{3/2}-u^{1/2} \, du= \frac{2}{5}u^{5/2}- \frac{2}{3}u^{3/2}+C

= \dfrac {2}{5}(x+1)^{5/2}- \dfrac{2}{3}(x+1)^{3/2}+C

Oct 20

Scientific notation on your calculator

By Tutor GuyNo Comments

 

To express numbers in scientific notation on your calculator, you should always use the EE key (EXP key on some calculators). Some calculators will insert a small capital E, others will display the exponents on the far right side of your calculator display. Remember that the E means “times ten to the…”. You should never write scientific notation numbers on your calculator with the caret key (such as 3.1 x 10^4).

Note that a number like (2.3)4 is not in scientific notation! It is not the same number as 2.3 x 104. The number in red is equal to 2.3 x 2.3 x 2.3 x 2.3. The number in blue is equal to 2.3 x 10,000. So for a number like (2.3)4, do not use the EE key.

Most scientific and graphing calculators let you change the display back and forth between regular notation and scientific notation. If you learn how to use this feature, you don’t have to count zeroes when you get an answer like 0.00000571. Just convert to scientific notation and the calculator tells you the number is 5.71 x 10-6.

Sep 29

Using l’Hôpital’s Rule

By Tutor GuyNo Comments

 

There are two guidelines you should always follow when applying l’Hôpital’s rule:

  • Make sure the original function gives you an indeterminate result before you take the derivatives;
  • Always simplify the result before plugging in to save yourself some extra work.

Example 1: Here’s a simple example that demonstrates the importance of the first guideline.

Find:

\displaystyle \lim_{x \to 0} \frac{x}{1+ \sin x}

 Solution: This function is continuous at x=0. To find the limit, simply plug in 0:

 \displaystyle \lim_{x \to 0} \frac{x}{1+ \sin x}=\frac{0}{1+0}=0

This is easily verified if you graph the function. However, if you try to apply l’Hôpital’s rule right away, you will get the incorrect value for the limit:

\displaystyle \lim_{x \to 0} \frac{x}{1+ \sin x}=\lim_{x \to 0} \frac{1}{\cos x}= \frac{1}{1}=1

 

Example 2: This example demonstrates the importance of the second guideline.

Find:

\displaystyle \lim_{x \to 0^+} \dfrac{\ln x}{^1 \!/ \!_x}

This satisfies the conditions for applying l’Hôpital’s rule, because plugging in gives an indeterminate form.

 

\displaystyle \lim_{x \to 0^+} \dfrac{\ln x}{^1 \!/ \!_x}=\frac{\ln 0}{^1 \! / _0}= \frac{-\infty}{\infty}

 We apply l’Hôpital’s rule once:

\displaystyle \lim_{x \to 0^+} \dfrac{\ln x}{^1 \!/ \!_x}= \lim_{x \to 0^+}\frac{1/x}{-1/x^2}

This would give us another indeterminate form if we plug in now, but we remember to simplify first, and it’s easy to evaluate:

 

\displaystyle \lim_{x \to 0^+} \dfrac{\ln x}{^1 \!/ \!_x}= \lim_{x \to 0^+}\frac{1/x}{-1/x^2}= \lim_{x \to 0^+} -x=0

Again, this is easy to verify by plotting the function.

Sep 26

Is it positive? increasing? concave up?

By Tutor GuyNo Comments

 

When you are asked to analyze a function in calculus, be sure to distinguish between positive/negative, increasing/decreasing, and concave up/concave down. These are three different concepts!

Here’s the same function, shown three times.

  • The value of the function determines whether it is positive or negative:

 

 

 

 

 

 

 

  • The value of the first derivative determines whether it is increasing or decreasing:

 

 

 

 

 

 

 

 

  • The value of the second derivative determines whether it is concave up or concave down:

Sep 01

Tangent lines to a curve

By Tutor GuyNo Comments

 

Imagine an ant riding a tiny railroad car along your function. There are lights on the rail car pointing straight ahead and straight back. The lights always point in the direction of the tangent line at that point.

In the function below, the blue line is tangent to the function at the point shown. As the ant walks along the function, his lights point along the tangent line.

 

 

 

 

 

 

 

 

 

Newer >
Blue Taste Theme created by Jabox