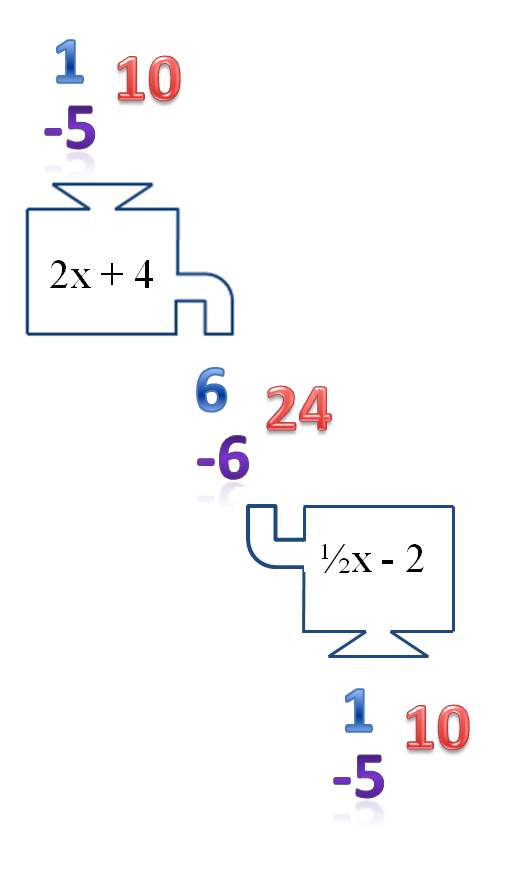
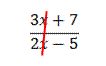Bay Area Tutoring

Graphing rational functions—2. Finding holes and vertical asymptotes

By Tutor GuyNo Comments

In a previous post, I listed the steps you need to follow to analyze and graph a rational function. In this post, I show you how to find the hole(s) and vertical asymptote(s), if they exist. [Check other posts on this website for other steps in analyzing and graphing a rational function.]

In a rational function, holes and vertical asymptotes will only occur where the denominator is equal to zero. So fully factor the function, and look for the roots of the denominator. When a factor in the denominator cancels out with a factor in the numerator, the function will have a hole where the factor equals zero. If the factor in the denominator does not cancel out with a factor in the numerator, there will be a vertical asymptote where the factor equals zero.

Example: Find the holes and vertical asymptotes, if any, for the following rational function:

$f(x)=\dfrac{x^2+3x+2}{x^3+4x^2+x-6}$

First, fully factor the function:

$f(x)=\dfrac{x^2+3x+2}{x^3+4x^2+x-6}=\dfrac{(x+1)(x+2)}{(x-1)(x+2)(x+3)}=\dfrac{(x+1)}{(x-1)(x+3)}$

The roots of the denominator are $-3$ , $-2$ and $1$ . At $x=-2$ , there is a hole. To find the “value” of the hole, evaluate the reduced function:

$f(-2)=\dfrac{(-2+1)}{(-2-1)(-2+3)}=\dfrac{-1}{-3}=\dfrac{1}{3}$

This means that when you graph the function, there will be a hole at the point $(-2, 1/3)$ .

The vertical asymptotes will be $x=-3$ and $x=1$ .

Aug 11

Graphing rational functions—1. Finding x- and y- intercepts

By Tutor GuyNo Comments

In a previous post, I listed the steps you need to follow to analyze and graph a rational function. In this and subsequent posts, I will walk you through each of those steps. Usually the first step in plotting a rational function is finding the $x$ – and $y$ -intercepts. You have done this before for other functions and the process here is no different.

To find the $y$ -intercept, set $x=0$ and solve for $f(x)$ .
To find the $x$ -intercept(s), set $f(x)=0$ and solve for $x$ . Recall that a rational function is a fraction, and a fraction can only be equal to zero when its numerator is equal to zero (as long as the denominator is not also equal to zero!). So in practice, you find the $x$ -intercept(s) by setting the numerator equal to zero and solving for $x$ .

Example: Find the $x$ – and $y$ -intercepts, if any, for the following rational function:

$f(x) = \dfrac{x^3+4x^2+x-6}{x^2+3x+2}$

Finding the $y$ -intercept is very easy if the polynomials are written in standard form as above. $f(0)$ is simply the ratio of the constant terms: $\frac{-6}{2} = -3$ . If the rational function has already been factored, you need to plug zero in to each term and evaluate.

To find the $x$ -intercept (and all the other parts of the rational function), the first thing you need to do is fully factor the numerator and denominator.

$f(x)=\dfrac{x^3+4x^2+x-6}{x^2+3x+2}=\dfrac{(x-1)(x+2)(x+3)}{(x+1)(x+2)}$

From here, it is easy to see that the roots of the numerator are $-3$ , $-2$ and $1$ . When $x=-2$ , the denominator is also zero, so this is not an $x$ -intercept; it is a hole. The $x$ ‑intercepts are at $-3$ and $1$ .

Is it possible that a rational function does not have a $y$ -intercept? Yes, if the function is not defined for $x=0$ . In other words, if a rational function has either a hole or a vertical asymptote at $x=0$ , there is no $y$ -intercept.

[Check out my other posts in this section that describe how to perform the other steps when analyzing a rational function.]

Aug 04

Graphing rational functions—overview

By Tutor GuyNo Comments

Graphing rational functions can be scary for a lot of students because there are so many details to manage. But you can make the process simpler by breaking down all the requirements into small steps. In this post I list all of the steps you should follow to analyze a rational function. Note that you can do these steps in any order. In subsequent posts, I will walk you through each of the steps and show you how to execute them.

Let’s start with the definition of a rational function. A rational function is a function that consists of a fraction, where both the numerator and denominator are polynomials. Or in symbols, if g(x) and h(x) are polynomials, then

$f(x)=\dfrac{g(x)}{h(x)}$

is called a rational function.

To analyze and graph a rational function, you need to do all of the following steps:

Find the y-intercept (if it exists)
Find the x-intercept(s) (if they exist)
Determine the location of holes, if any
Find the vertical asymptotes, if any
Find the horizontal or oblique asymptotes, if any
Determine the end behavior (if no horizontal or oblique asymptotes)

[Note that this is a list for algebra 2 and precalc students. When you get to calculus, there will be additional steps to completely analyze the function.]

This probably feels like a long and complicated list, but for the most part, each step by itself is not very difficult. Just perform each step in turn and you can become an expert at rational functions. Check out my other posts in this section that describe how to perform each of these steps.

Jul 21

The Most Common Factoring Mistake

By Tutor GuyNo Comments

I am surprised (and a little disappointed) every year when one of my students tries to simplify a polynomial fraction by cancelling out terms that can’t be cancelled out. For example, when faced with

$\dfrac{3x+7}{2x-5}$

inevitably, a student will ask me, “Can I cancel out the x’s like this?”

Tears well up in my eyes as I explain that no, the x’s do not cancel. I explain patiently why the x’s do not cancel. And very often, the next time I work with that student, he or she will try to cancel out the x’s again. This is the most common factoring mistake I see students make, and it’s not limited to Algebra students. I’ve even seen Calculus student make this error. That usually makes me sob quite loudly.

If you would like to keep me from crying, then you need to learn how to simplify polynomial fractions. It’s quite simple once you understand that terms that are added do not cancel out. Only factors that are multiplied together can cancel. Let’s start by looking at a fraction with numbers and no variables.

$\dfrac{210}{462}$

Can this be simplified? Of course. Most students will divide the top and bottom by 2, then by 3, and then by 7, as follows:

$\dfrac{210}{462}=\dfrac{105}{231}=\dfrac{35}{77}=\dfrac{5}{11}$

This is correct. But why can you cancel out a 2 and a 3 and a 7? It’s because they are factors of the numerator and the denominator. Let’s do the same problem by completely factoring the top and bottom first:

$\dfrac{210}{462}=\dfrac{2\cdot 3 \cdot 5 \cdot 7}{2 \cdot 3 \cdot 7 \cdot 11}=\dfrac{5}{11}$

When you write it out like this, you can see that the 2’s cancel, the 3’s cancel, and the 7’s cancel. And they cancel only because they are factors.

Now let’s try to simplify some polynomial fractions. Start by factoring the numerator and denominator completely, then any like factors will cancel:

$\dfrac{2x-4}{6x+14}=\dfrac{2(x-2)}{2(x+7)}=\dfrac{x-2}{x+7}$

$\dfrac{4x+8}{12x+24}=\dfrac{4(x+2)}{12(x+2)}=\dfrac{4}{12}=\dfrac{1}{3}$

$\dfrac{x^2-1}{x^2+4x+3}=\dfrac{(x+1)(x-1)}{(x+1)(x+3)}=\dfrac{x-1}{x+3}$

Oct 20

Scientific notation on your calculator

By Tutor GuyNo Comments

To express numbers in scientific notation on your calculator, you should always use the EE key (EXP key on some calculators). Some calculators will insert a small capital E, others will display the exponents on the far right side of your calculator display. Remember that the E means “times ten to the…”. You should never write scientific notation numbers on your calculator with the caret key (such as 3.1 x 10^4).

Note that a number like (2.3)⁴ is not in scientific notation! It is not the same number as 2.3 x 10⁴. The number in red is equal to 2.3 x 2.3 x 2.3 x 2.3. The number in blue is equal to 2.3 x 10,000. So for a number like (2.3)⁴, do not use the EE key.

Most scientific and graphing calculators let you change the display back and forth between regular notation and scientific notation. If you learn how to use this feature, you don’t have to count zeroes when you get an answer like 0.00000571. Just convert to scientific notation and the calculator tells you the number is 5.71 x 10^-6.

Oct 17

Solving sin x equations

By Tutor GuyNo Comments

“Sine” is a function, not a number. Sin (x) does not mean ‘sine times x’. New trig students often want to solve an equation like sin x = 0.5 by ‘dividing by sine’. This would be like solving

$\sqrt{x}=6 \text{ as } x= \dfrac{6}{\sqrt{\text{ }}}$

It’s completely meaningless! Instead, you need to take the inverse sine of both sides:

$\sin x=0.5$

$\sin^{-1}$ $\sin x =$ $\sin^{-1}$ $0.5=30 \textdegree$

Oct 13

What are inverse functions?

By Tutor GuyNo Comments

The inverse of a function undoes whatever the original function did. If you plug a number into a function and then plug the result of this into the inverse, you always get back what you started with.

Think of a function as a machine that operates on a number. You put in a value for x, the machine performs the rule defined by f(x), and the machine then spits out the new value.

The inverse function, written f ^-1(x), is the function that reverses all the operations and gives you the original number back. You can think of it as turning the function machine upside down and running the number through it backwards:

As an example, let’s say that f(x) = 2x + 4. If you put in 1, the machine gives out 6; if you put in 10, the machine gives out 24; if you put in -5, the machine gives -6.

The inverse function for 2x + 4 is ½x – 2. If you put 6, 24, and -6 into this function, you get back the numbers you started with!

You can always show that two functions are inverses of each other by showing that
f(f^‑1(x)) = x or f^‑1(f(x)) = x. Using the example above:

f(f^-1(x)) = 2(½x – 2) + 4 = x – 4 + 4 = x.

Oct 06

Degrees vs. radians: which is “better”?

By Tutor GuyNo Comments

Both degrees and radians have their uses and you are probably more familiar with degrees, but only because you learned them first. By the time you get to calculus, you have to work in radians, so you need to be comfortable with them. And they’re not as confusing as they seem. Just as you can measure your height in inches or in centimeters, degrees and radians are just two different ways of measuring angles.

Trig will be easier if you learn to count in both degrees and radians. You probably already know that there are 360° in a circle. Now memorize that there are also 2π radians in a circle.

The only conversion you have to remember is that π radians = 180°. Then you can determine all the other special angles pretty quickly. For example, π/6 rad = 180°/6 = 30°. π/4 rad = 180°/4 = 45°. It’s that simple!

Sep 22

Inverse of a 2×2 matrix

By Tutor GuyNo Comments

$\left ( \begin{bmatrix} a & b \\ c & d \end{bmatrix} \right )^{-1} = \text{ ?}$

Instead of calculating the inverse of a 2 x 2 matrix, it’s easier to remember this simple manipulation:

Switch the a and d terms, and
change the signs on the b and c terms.
Then divide every term by the determinant $(ad - bc).$ The result will be the inverse of the original matrix.

In general:

$\left ( \begin{bmatrix} a & b \\ c & d \end{bmatrix} \right )^{-1} = \dfrac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}$

Example:

$\left ( \begin{bmatrix} 2 & 1 \\ -3 & 7 \end{bmatrix} \right )^{-1} = \dfrac{1}{2 \cdot 7-1 \cdot (-3)} \begin{bmatrix} 7 & -1 \\ 3 & 2 \end{bmatrix} = \dfrac{1}{17} \begin{bmatrix} 7 & -1 \\ 3 & 2 \end{bmatrix}= \begin{bmatrix} ^7 \! / _{17} & ^{-1} \! / \! _{17} \\ ^3 \! / \! _{17} & ^2 \! / \! _{17} \end{bmatrix}$

Sep 19

Matrix multiplication

By Tutor GuyNo Comments

To multiply matrices, always multiply a row of the left matrix with a column of the right matrix. It helps to picture the column of the second matrix “flying out” of its matrix and hovering over the row of the first matrix, so you can do the multiplication quickly and easily.

Example:

Let’s say you are going to multiply the first row of the first matrix by the second column of the second matrix:

In your mind, place the column over the row to line up the corresponding elements:

Then you can quickly calculate (1 · 2) + (-4 · 3) + (2 · 4) = -2.

Archive

For the Precalc/Trig category

Graphing rational functions—2. Finding holes and vertical asymptotes

Graphing rational functions—1. Finding x- and y- intercepts

Graphing rational functions—overview

The Most Common Factoring Mistake

Scientific notation on your calculator

Solving sin x equations

What are inverse functions?

Degrees vs. radians: which is “better”?

Inverse of a 2×2 matrix

Matrix multiplication

Tutor Guy Homework Tips