Archive

The blog archives.

Sep 19

Matrix multiplication

By Tutor GuyNo Comments

 

To multiply matrices, always multiply a row of the left matrix with a column of the right matrix. It helps to picture the column of the second matrix “flying out” of its matrix and hovering over the row of the first matrix, so you can do the multiplication quickly and easily.

Example:

Let’s say you are going to multiply the first row of the first matrix by the second column of the second matrix:

 

 

 

In your mind, place the column over the row to line up the corresponding elements:

 

 

 

 

Then you can quickly calculate (1 · 2) + (-4 · 3) + (2 · 4) = -2.

Sep 15

Trig functions: positive or negative?

By Tutor GuyNo Comments

 

Many students like to use the phrase “All Students Take Calculus” to help them remember where the various trig functions are positive or negative. Place the letters of these four words in quadrants I to IV as shown below.

  • The A in Quadrant I stands for “all functions” (sine, cosine & tangent) are positive in this quadrant.
  • The S in Quadrant II stands for “only sine” is positive in this quadrant.
  • The T in Quadrant III stands for “only tangent” is positive in this quadrant.
  • The C in Quadrant IV stands for “only cosine” is positive in this quadrant.

 

Another simple method is to remember that the cosine values are the x coordinates on the unit circle (and therefore positive in Quadrants I and IV) and the sine values are the y coordinates (and therefore positive in Quadrants I and II).

Sep 12

The Unit Circle

By Tutor GuyNo Comments

 

The sooner you memorize the sine, cosine and tangent of the special angles on the unit circle, the easier trig will be for you. Yes, you can always derive these values from the rules for special triangles you learned in geometry, but that is no substitute for memorizing the unit circle.

Sep 08

Taming trig identities

By Tutor GuyNo Comments

 

Proving trig identities is not as difficult as it looks if you follow these strategies.

1. The first thing you should look for is to factor one or both sides like a polynomial. This is not always possible, but simplifies the rest of the work.

2. If there are double angle functions [such as sin(2θ)] or sum of angle functions [such as sin(α + β)], expand these using the double angle or sum formulas.

3. Look for trig identities, and substitute them to simplify the expression.

4. If one side of the identity has two fractions added or subtracted, combine the fractions by finding a common denominator. (Then look for factors or identities as above.)

5. When in doubt, convert everything to sines and cosines. Then try to simplify the resulting expression.

6. If the expression contains 1 + sin θ or 1 + cos θ, consider multiplying top and bottom by the “conjugate”: 1 – sin θ or 1 – cos θ. This will give you a trig identity you can simplify.

7. When you get one side as simple as it can get, start on the other side.

8. Don’t give up! If you aren’t making the expression simpler, cross it out and try another strategy.

 

Example: Here’s a (rather complicated) example. Don’t panic! Watch how we can use all of the strategies above to solve the identity step by step.

Prove the identity:

\dfrac{2 \tan \theta + 2 \sin \theta \tan \theta}{\sec \theta \sin 2 \theta}= \dfrac{\cos^3 \theta}{2-2 \sin \theta} \left ( \dfrac{1}{1- \sin \theta}+ \dfrac{1}{1+ \sin \theta} \right )

 Think you can do it? Sure you can! The first thing you do is factor. Start with the left side, and you see you can factor 2 tan θ out of the numerator:

\dfrac{2 \tan \theta (1+ \sin \theta)}{\sec \theta \sin 2 \theta}= \dfrac{\cos^3 \theta}{2-2 \sin \theta} \left ( \dfrac{1}{1- \sin \theta}+ \dfrac{1}{1+ \sin \theta} \right )

 Strategy 2 says to expand double angle formulas.  Change the sin 2θ in the denominator:

\dfrac{2 \tan \theta (1+ \sin \theta)}{\sec \theta (2 \sin \theta \cos \theta)}= \dfrac{\cos^3 \theta}{2-2 \sin \theta} \left ( \dfrac{1}{1- \sin \theta}+ \dfrac{1}{1+ \sin \theta} \right )

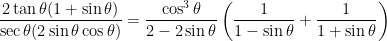
 There are no identities on the left side (strategy 3), so go to strategy 4 and convert the tan θ and sec θ into sines and cosines:

\dfrac{2 \sin \theta \cos \theta (1+ \sin \theta)}{\cos \theta (2 \sin \theta \cos \theta)}= \dfrac{\cos^3 \theta}{2-2 \sin \theta} \left ( \dfrac{1}{1- \sin \theta}+ \dfrac{1}{1+ \sin \theta} \right )

 Now let’s simplify the left side before moving on:

\dfrac{1+ \sin \theta}{\cos \theta}= \dfrac{\cos^3 \theta}{2-2 \sin \theta} \left ( \dfrac{1}{1- \sin \theta}+ \dfrac{1}{1+ \sin \theta} \right )

 That’s about as simple as you can make the left side.  Strategy 7 says to move to the other side. The first thing to do is factor a 2 out of the 2 – 2 sin θ term in the denominator:

\dfrac{1+ \sin \theta}{\cos \theta}= \dfrac{\cos^3 \theta}{2(1-\sin \theta)} \left ( \dfrac{1}{1- \sin \theta}+ \dfrac{1}{1+ \sin \theta} \right )

 Next, strategy 4 says to combine the sum of the two fractions by finding a common denominator:

\dfrac{1+ \sin \theta}{\cos \theta}= \dfrac{\cos^3 \theta}{2(1-\sin \theta)} \left ( \dfrac{1+ \sin \theta}{(1- \sin \theta)(1+ \sin \theta)}+ \dfrac{1- \sin \theta}{(1- \sin \theta)(1+ \sin \theta)} \right )

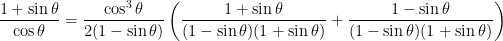
 Let’s simplify that mess in the parentheses (notice that we multiply out the two factors in the denominator):

\dfrac{1+ \sin \theta}{\cos \theta}= \dfrac{\cos^3 \theta}{2(1-\sin \theta)} \left ( \dfrac{2}{1- \sin^2 \theta} \right )

 Now we have an identity (strategy 3)! Substitute cos2 θ for 1-sin2 θ in the denominator and cancel with the cos3 θ. Cancel the 2 on the top and bottom also:

\dfrac{1+ \sin \theta}{\cos \theta}= \dfrac{\cos \theta}{1-\sin \theta}

 We’ve simplified both sides significantly, but they’re not the same yet. Here’s where we apply strategy 6 by multiplying top and bottom of the left side by 1 – sin θ and simplifying:

\dfrac{1- \sin \theta}{1- \sin \theta} \cdot \dfrac{1+ \sin \theta}{\cos \theta}= \dfrac{\cos \theta}{1-\sin \theta}

\dfrac{1- \sin^2 \theta}{(1- \sin \theta) \cos \theta} = \dfrac{\cos \theta}{1-\sin \theta}

\dfrac{\cos^2 \theta}{(1- \sin \theta) \cos \theta} = \dfrac{\cos \theta}{1-\sin \theta}

\dfrac{\cos \theta}{1- \sin \theta} = \dfrac{\cos \theta}{1-\sin \theta}

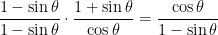
 Hey, we did it! We have tamed a very difficult identity by methodically applying the strategies at the top of this page one after another!

Sep 05

Exponents and logarithms

By Tutor GuyNo Comments

 

The two equations y = bx and logb y = x are equivalent. They mean the same thing.

The first equation is called the exponential form and the second is called the logarithmic form. Many logarithm problems can be made much simpler by converting them to exponential form. If you can convert back and forth between these two forms, you will find exponential and logarithm problems easier to solve.

Example 1: Solve: log2 (x2) = 6.

Solution:  Rewrite the problem in exponential form:

26 = x2 → 64 = x2 → x = ±8.

Example 2: Solve: ex = 35.

Solution: Rewrite the problem in logarithmic form:

ln 35 = x  → x ≈ 3.56.

Sep 01

Tangent lines to a curve

By Tutor GuyNo Comments

 

Imagine an ant riding a tiny railroad car along your function. There are lights on the rail car pointing straight ahead and straight back. The lights always point in the direction of the tangent line at that point.

In the function below, the blue line is tangent to the function at the point shown. As the ant walks along the function, his lights point along the tangent line.

 

 

 

 

 

 

 

 

 

Aug 30

Finding angles in radians

By Tutor GuyNo Comments

 

Finding the location of an angle on the unit circle in radians is a lot easier if you imagine counting in multiples of π/2, π/3, π/4 or π/6. For example, to figure out where 5π/3 is on the unit circle, count out “one π/3, two π/3, three π/3 (which is π), four π/3, five π/3.” You’ll get to the right spot every time!

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Of course, to make this process work, you do need to know the following relationships

  • π/2 = 90°
  • π/3 = 60°
  • π/4 = 45°
  • π/6 = 30°
Aug 25

Biconditional statements

By Tutor GuyNo Comments

 

When a conditional and its converse are both true, we call this a biconditional. A biconditional means that the hypothesis is true if and only if the conclusion is true. [Some math teachers like to abbreviate ‘if and only if’ as ‘iff’.]

It is also appropriate to call a biconditional statement a definition, because it says the hypothesis and the conclusion imply each other (so they are the same thing).

Here’s an example of a biconditional:

Conditional:  If an angle is a right angle, then it has a measure of 90°.

Converse: If an angle has a measure of 90°, then it is a right angle.

Both of these statements are true, and so we could also call this a definition: A right angle is an angle with a measure of 90°.

Aug 22

Mastering geometry proofs

By Tutor GuyNo Comments

 

A good strategy for completing a proof in geometry is to work backwards. If you are having trouble determining where to start, try going to the end first. Look at the statement you are trying to prove and ask yourself, “What do I need to know in order to prove this statement?” In other words, what would the last line of the proof be? Then figure out what you need in order to prove the next to last line of the proof, and so on.

Here’s an example to show how this works:

Given: \overline{AE} and \overline{BD} bisect each other.
Prove: \overline{AB} \cong \overline{DE}.

 

 

 

 

 

 

 

 

 

How do you approach this? The first question to ask yourself is “what do I need to know to prove the two segments are congruent?” The answer: Show that the two triangles are congruent—then the segments will be congruent by CPCTC.

So next, the question becomes “how do I show that the triangles are congruent?” Well, you can show triangles are congruent with SSS, SAS or ASA.

Continuing to work backwards, the next question is “can I prove SSS?” Well, no, because you’re trying to prove two sides are congruent. You can’t use what you’re trying to prove in a congruence proof! So ask the next question: “can I prove SAS?” And the answer is yes!

Because \overline{AE} and \overline{BD} bisect each other, \overline{AC} \cong \overline{CE} and \overline{BC} \cong \overline{CD}.    And \angle{ACB} \cong \angle{DCE}  because they are vertical angles.

You have simplified the proof to finding two congruent sides and a congruent angle. This leads to SAS which leads to two congruent triangles which leads to the two congruent segments you were trying to prove.

Aug 17

Finding the missing acute angle in a right triangle

By Tutor GuyNo Comments

 

In a right triangle, the two acute angles add up to 90°. If you are trying to find one missing angle, it’s usually easier to find the complement of the other acute angle than to subtract the two known angles from 180°.

Example: Find angle A. 

 

 

 

 

 

 

 

 

 

Solution: Since this is a right triangle, A and B add up to 90. Therefore, 90 – 63 = 27°.

< OlderNewer >
Blue Taste Theme created by Jabox