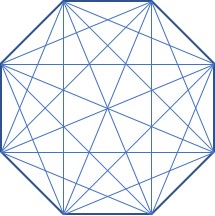
How many diagonals are there in an octagon?
Instead of trying to count them all, use the formula for the number of diagonals in any polygon:
where n = the number of sides and d= the number of diagonals. For an octagon, n= 8, so
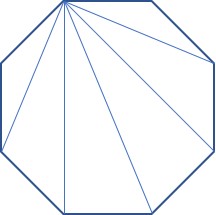
This is a good formula to memorize and its derivation is pretty simple, so let’s see it. We will use the same octagon diagram, but only draw the diagonals from one vertex:
You can see that from this vertex on the upper left, a diagonal can be drawn to every vertex except the two adjacent vertices and to itself. So the number of diagonals from any vertex in an n-gon is (n-3). Since there are n vertices, the total number of diagonals is n(n-3). But we’ve just counted every diagonal twice (once from each endpoint), so to find the number of different diagonals, we divide by two. This gives us the formula above.