Archive

For the Physics category

Dec 15

Pulley problems

By Tutor GuyNo Comments

 

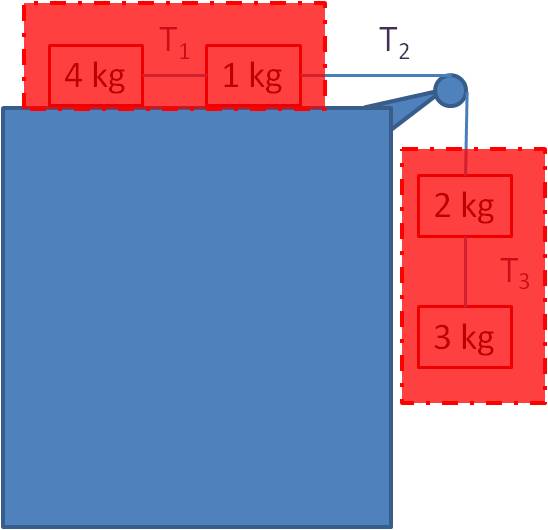
In a pulley problem, if you have a chain of boxes all connected by ropes, first find the tension in the rope that goes over the pulley (treat all of the boxes on the table as a single box and all of the boxes hanging down as a single box). Then work your way to each end of the chain one box at a time to find the tension in each rope along the chain.

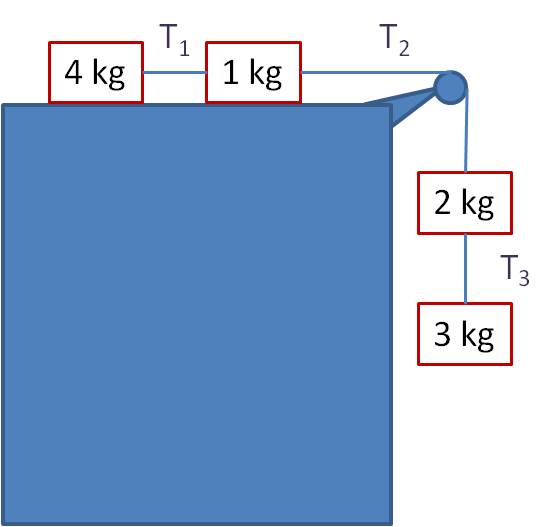
Example: Find the tensions in each cable and the acceleration of the blocks in the diagram below. Assume that the pulley is massless and the table and pulley are frictionless.

 

 

 

 

 

 

 

 

 

 

 

 

Solution: First, treat the two blocks on the table as a single unit of 5 kg, and treat the two hanging blocks as a single unit of 5 kg:

 

 

 

 

 

 

 

 

 

 

 

 

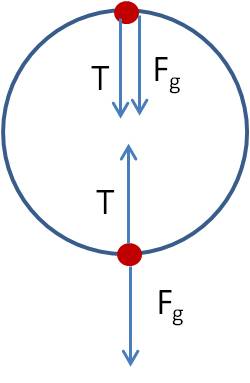
The net force equation for the “block” on the table is:

T2 = ma = 5a                                (1)

The net force equation for the hanging “block” is:

mg – T2 = ma → 5g – T2 = 5a             (2)

Plugging equation (1) into equation (2) gives

a = g/2 = 4.9 m/s2 and T2 = 5g/2 = 24.5 N.

Now you can find the other tensions. Find T3 by doing an FBD on the 3 kg block:

3g – T3 = 3a = 3g/2

Solve to get T3 = 3g/2 = 14.7 N. Find T1 by doing an FBD on the 4 kg block:

T1 = 4a = 2g, so T1 = 19.6 N.

Dec 12

Solving uniform circular motion problems

By Tutor GuyNo Comments

 

In order for an object to move in a uniform circular path, the net force on the object must be mv2/r. Draw the FBD, and any forces not pointed along a radius of the circle must cancel out.  All the remaining forces must add up to mv2/r.

Example 1: You attach a ball to the end of a rope and swing it around vertically in a circle. If the rope is 0.50 m long, the ball has a mass of 0.50 kg, and the ball is traveling at a constant speed of 6.0 m/s, what is the tension in the rope at the bottom of the circle? At the top of the circle?

Solution: The FBD is shown for the ball at the bottom of the circle and at the top (I’ve shown the ball in its orbit, but left out the rope to make the picture clearer). Let’s solve the bottom case first.

 

 

 

 

 

 

 

 

 

 

 

 

The net force is T– Fg. Since the ball is traveling in a circle, the net force must be the centripetal force that keeps the ball in a circle, so

T-F_g= \dfrac{mv^2}{r} \rightarrow T= \dfrac{mv^2}{r}+mg \rightarrow T= \dfrac{(0.5)(6.0)}{(0.5)}+(0.5)(9.8)=10.9 \, N

 Finding the solution at the top of the circle is just as simple:

T+F_g= \dfrac{mv^2}{r} \rightarrow T= \dfrac{mv^2}{r}-mg \rightarrow T= \dfrac{(0.5)(6.0)}{(0.5)}-(0.5)(9.8)=1.1 \, N

 Note that in problems like this one, the tension is greatest at the bottom and a minimum at the top.

Example 2 : One of the obstacles at your favorite miniature golf course is a loop-the-loop as seen in the picture below. What is the minimum velocity necessary for the golf ball to stay in contact with the loop-the-loop at the top of the loop? The loop has a radius of 1.0 m.

 

 

 

 

 

 

 

Solution: Draw an FBD of the situation.

 

 

 

 

 

 

 

The two forces on the golf ball are the force due to gravity and the normal force of the loop against the golf ball. As in the last example, we set the net force equal to the centripetal force.

F_N+F_g= \dfrac{mv^2}{r}

 You can see from this equation that minimizing the velocity means minimizing the two forces. If the normal force is zero (i.e., if the ball is just barely making contact with the loop, this satisfies our requirement:

0+mg= \dfrac{mv^2}{r} \rightarrow v= \sqrt{rg} \rightarrow v= \sqrt{(1)(9.8)}=3.1 \, m/s

 Note that the answer does not depend on the mass of the golf ball!

Nov 24

Free Body Diagrams when velocity is constant

By Tutor GuyNo Comments

 

Acceleration is the rate of change of the velocity. So if you are told that an object is stationary or is moving at constant velocity, this means the acceleration is zero. From Newton’s Second Law (F = ma), if the acceleration is zero, this means the net force is zero. So whenever velocity is constant, all the forces in the x and y directions must cancel out! Here’s a problem that shows how this concept is a powerful tool for solving free body problems:

Example: Jack pushes a large crate across a level surface at a constant speed. The crate has a mass of 50 kg and Jack exerts a horizontal force of 200 N. What is the coefficient of friction, μ?

 

 

 

 

 

 

Answer: It seems that we don’t have enough information because we don’t know the velocity of the crate. But the fact that the speed is constant tells us that the net force is zero. So the solution is straightforward. First draw the free body diagram:

 

 

 

 

 

 

 

 

 

 

 

Because the net force is zero, the weight Fg is equal in magnitude to FN.

F_N=F_g=mg=(50)(9.8)=490 \, N

And because the net force is zero, the force Jack exerts is equal in magnitude to the frictional force.

F_f= \mu F_N=F \rightarrow \mu (490)=200 \rightarrow \mu = 0.41

Nov 21

Finding the angles of the gravity components in a ramp problem

By Tutor GuyNo Comments

 

In a ramp (or inclined plane) problem, the angle of the ramp is the same as the angle the gravity vector makes with the component normal to the ramp.

 

 

 

 

 

 

 

 

Here’s how you can be sure this is true: Look at the component of the gravity vector that is perpendicular to the ramp. Imagine that the ramp is horizontal—that is, θ is currently 0. Then the perpendicular component points straight down so that it coincides with Fg. Now start lifting the ramp. As the ramp angle increases, so does the angle between the perpendicular component and the gravity vector. You can see that these two angles have to be the same.

Nov 17

Units vs. Quantities in electromagnetism

By Tutor GuyNo Comments

 

Keeping the abbreviations straight in electromagnetism is particularly hard because sometimes the abbreviation we use for a QUANTITY is the same letter we use to define a UNIT of a different quantity. For example, a capital C is used for capacitance in the equation C = Q/V. But in the statement Q = 0.050 C, the C stands for ‘coulomb’, the unit of charge. It is up to you to understand from the context whether the symbol refers to a quantity or a unit.

Also, the symbol for a QUANTITY often comes from a German abbreviation, so it’s not the letter you expect. For example, the symbol for inductance is L, not I, and the symbol for current is I, not C. Again, it’s up to you to learn these well enough that you can figure them out on your own. Here’s a table that shows the various symbols:

Quantity

Symbol   for quantity

Unit

Symbol   for unit

force

F

newton

N

charge

Q

coulomb

C

electric field

E

N/C or V/m

current

I

ampere

A

potential difference

V

volt

V

resistance

R

ohm

Ω

power

P

watt

W

capacitance

C

farad

F

magnetic flux

Φ

weber

Wb

inductance

L

henry

H

magnetic field

B

tesla

T
Nov 14

Mastering units in electromagnetism

By Tutor GuyNo Comments

 

Almost all of the units we use in electromagnetism are named after dead physicists, so they can be difficult to remember and distinguish. Consider making a flash card with a list of all the quantities and units as a quick reference guide until you have them memorized.

Quantity

SI   Unit

Symbol

Equivalent   units

force

 newton

N

 kg·m/s2

charge

 coulomb

C

 A·s
current ampere

A

potential difference

 volt

V

resistance

 ohm

Ω

 V/A
power watt

W

V·A
capacitance farad

F

A·s/V

magnetic flux

 weber

Wb

V·s

inductance

 henry

H

V·s/A
magnetic field tesla

T

Wb/m2
Oct 20

Scientific notation on your calculator

By Tutor GuyNo Comments

 

To express numbers in scientific notation on your calculator, you should always use the EE key (EXP key on some calculators). Some calculators will insert a small capital E, others will display the exponents on the far right side of your calculator display. Remember that the E means “times ten to the…”. You should never write scientific notation numbers on your calculator with the caret key (such as 3.1 x 10^4).

Note that a number like (2.3)4 is not in scientific notation! It is not the same number as 2.3 x 104. The number in red is equal to 2.3 x 2.3 x 2.3 x 2.3. The number in blue is equal to 2.3 x 10,000. So for a number like (2.3)4, do not use the EE key.

Most scientific and graphing calculators let you change the display back and forth between regular notation and scientific notation. If you learn how to use this feature, you don’t have to count zeroes when you get an answer like 0.00000571. Just convert to scientific notation and the calculator tells you the number is 5.71 x 10-6.

Newer >
Blue Taste Theme created by Jabox