Both degrees and radians have their uses and you are probably more familiar with degrees, but only because you learned them first. By the time you get to calculus, you have to work in radians, so you need to be comfortable with them. And they’re not as confusing as they seem. Just as you can measure your height in inches or in centimeters, degrees and radians are just two different ways of measuring angles.
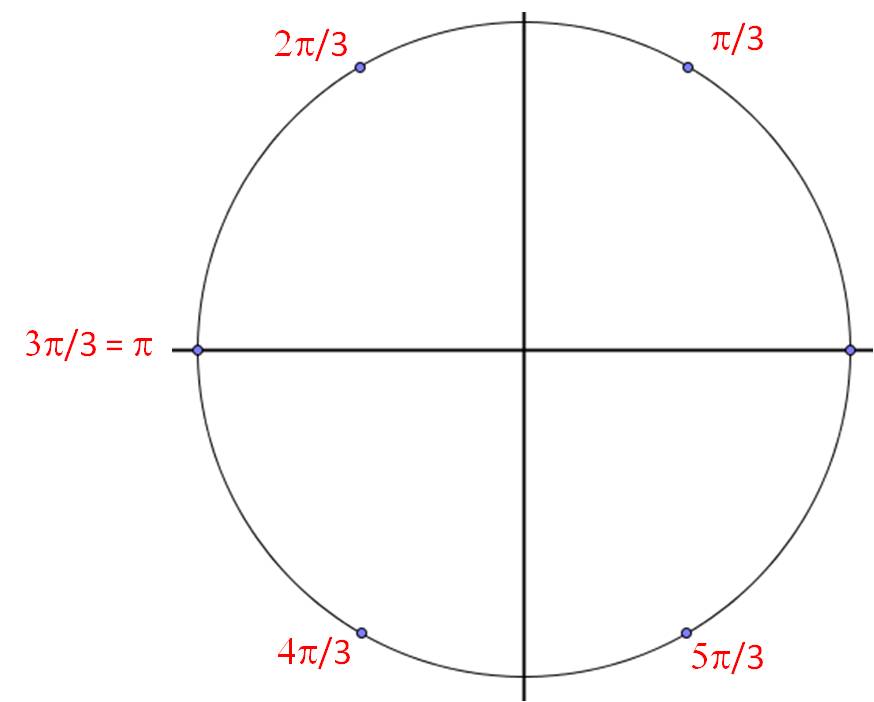
Trig will be easier if you learn to count in both degrees and radians. You probably already know that there are 360° in a circle. Now memorize that there are also 2π radians in a circle.
The only conversion you have to remember is that π radians = 180°. Then you can determine all the other special angles pretty quickly. For example, π/6 rad = 180°/6 = 30°. π/4 rad = 180°/4 = 45°. It’s that simple!