Bay Area Tutoring

When you are asked to sketch the graph of a polynomial, you do not want to make a tree to calculate the values of various points. You don’t know where the “turning points” are, so you won’t be able to connect the dots for the points you plot. Instead, you need to fully factor the polynomial and use the zeroes you find to draw the polynomial. In addition, the multiplicity of each factor tells you whether the polynomial crosses the -axis at that zero or “bounces”. The rule is very simple: If the factor has an odd multiplicity, the graph crosses the -axis. If the multiplicity is even, the graph bounces.

multiplicity	behavior at ‑axis
odd	crosses
even	bounces

Example: Sketch the graph of

Solution: First of all, plot the zeroes. For this problem, the zeroes are at

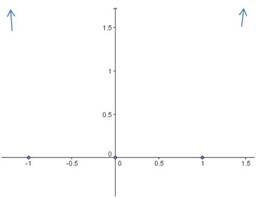
Next, determine the degree of the polynomial. In this case, it is degree . (Add the exponents of all the factors: ) The degree tells you the end behavior, and you can draw arrows to show that the function will go to positive infinity on the left and the right.

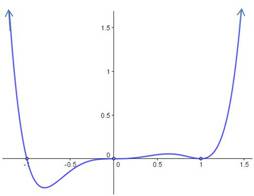
Now you can sketch the graph. At the zero is multiplicity 1, so the graph crosses the -axis. At the zero is multiplicity 3, so the graph also crosses the -axis. Note that for multiplicity 3, the graph doesn’t cross straight through the axis, but flattens out as it goes through. At the zero is multiplicity 2, so the graph bounces at the -axis. The final sketch is shown below: