Archive

The blog archives.

Oct 24

Factoring the sum or difference of two cubes

By Tutor GuyNo Comments

 

The sum or difference of two cubes can always be factored as follows:

(x^3+y^3)=(x+y)(x^2-xy+y^2)

(x^3-y^3)=(x-y)(x^2+xy+y^2)

 These formulas are not too easy to figure out on your own, so your best approach is to memorize them. But how do you keep straight where the plus and minus signs go? Some students like to use the acronym “SOAP”, which stands for Same-Opposite-Always Positive. This means that the first sign is the same as the sign in the sum or difference of the cubes, the second sign is the opposite of this sign, and the third sign is always positive.

Oct 20

Scientific notation on your calculator

By Tutor GuyNo Comments

 

To express numbers in scientific notation on your calculator, you should always use the EE key (EXP key on some calculators). Some calculators will insert a small capital E, others will display the exponents on the far right side of your calculator display. Remember that the E means “times ten to the…”. You should never write scientific notation numbers on your calculator with the caret key (such as 3.1 x 10^4).

Note that a number like (2.3)4 is not in scientific notation! It is not the same number as 2.3 x 104. The number in red is equal to 2.3 x 2.3 x 2.3 x 2.3. The number in blue is equal to 2.3 x 10,000. So for a number like (2.3)4, do not use the EE key.

Most scientific and graphing calculators let you change the display back and forth between regular notation and scientific notation. If you learn how to use this feature, you don’t have to count zeroes when you get an answer like 0.00000571. Just convert to scientific notation and the calculator tells you the number is 5.71 x 10-6.

Oct 17

Solving sin x equations

By Tutor GuyNo Comments

 

“Sine” is a function, not a number. Sin (x) does not mean ‘sine times x’. New trig students often want to solve an equation like sin x = 0.5 by ‘dividing by sine’. This would be like solving

\sqrt{x}=6 \text{ as } x= \dfrac{6}{\sqrt{\text{ }}}                           

 It’s completely meaningless! Instead, you need to take the inverse sine of both sides:

\sin x=0.5

\sin^{-1} \sin x = \sin^{-1} 0.5=30 \textdegree

Oct 13

What are inverse functions?

By Tutor GuyNo Comments

 

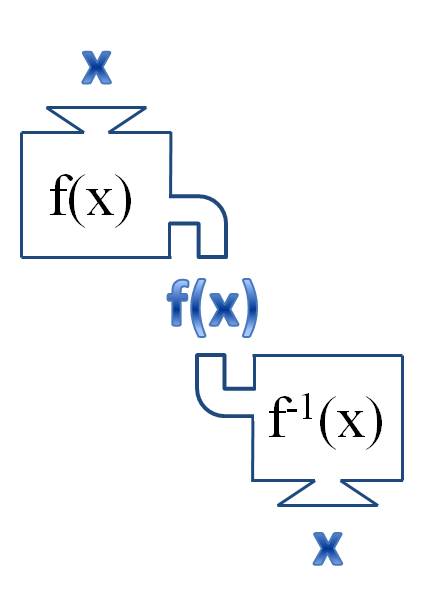
The inverse of a function undoes whatever the original function did. If you plug a number into a function and then plug the result of this into the inverse, you always get back what you started with.

Think of a function as a machine that operates on a number. You put in a value for x, the machine performs the rule defined by f(x), and the machine then spits out the new value.

 

 

 

The inverse function, written f -1(x), is the function that reverses all the operations and gives you the original number back. You can think of it as turning the function machine upside down and running the number through it backwards:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

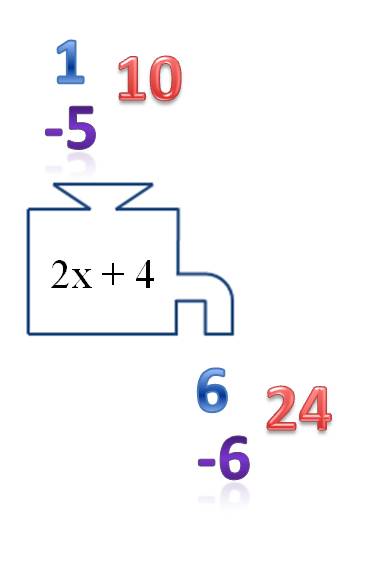
As an example, let’s say that f(x) = 2x + 4. If you put in 1, the machine gives out 6; if you put in 10, the machine gives out 24; if you put in -5, the machine gives -6.

 

 

 

 

 

 

 

 

 

 

 

 

 

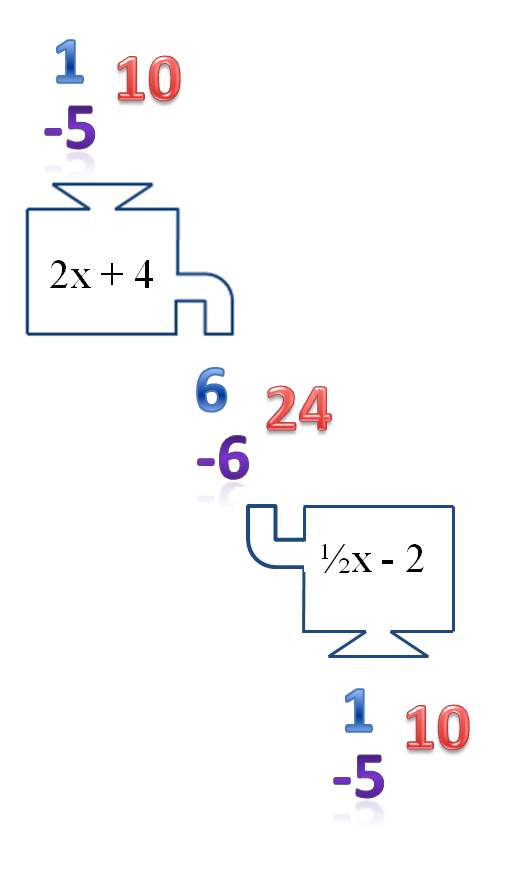
The inverse function for 2x + 4 is ½x – 2. If you put 6, 24, and -6 into this function, you get back the numbers you started with!

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

You can always show that two functions are inverses of each other by showing that
f(f ‑1(x)) = x or f ‑1(f(x)) = x. Using the example above:

f(f -1(x)) = 2(½x – 2) + 4 = x – 4 + 4 = x.

Oct 10

Strategies for succeeding in Statistics

By Tutor GuyNo Comments

 

Statistics can be a frustrating class for a lot of students because the rules often seem arbitrary and the formulas seem to come out of nowhere. You can stay on top of the work if you stay focused on the big picture. Here are two key ideas I stress to my Stats students at the beginning of every year:

  • Statistics deals with uncertainty. Unless we have the entire population in front of us (a very rare occurrence!), we can only make educated guesses about the data and the likelihood of particular events. In every other math class you’ve ever taken, you can find the exact answer. In statistics, you can only make predictions or calculate probabilities. All of the formulas we learn in Statistics are used to help us describe how the data varies and to make estimates for how likely an event is.
  • Statistics is not intuitive. In most of your math classes, you can usually tell if the answer you’ve gotten is reasonable or not. In Statistics, your best guess for what a particular probability should be may be way off the actual answer. That means if you have set up a problem incorrectly, you don’t get any feedback to help you. You have to learn which formula to use in which situation and then trust your calculator. That can be very scary!

My favorite example of how statistics is not intuitive is a famous problem known as the Birthday Paradox. Let’s say all of the students in your Statistics class were chosen at random from a large population. What is the probability that two students in the class share the same birthday? When I pose this question to my Stats students, I get guesses that range from 1% to about 20%. These seem like very “reasonable” guesses, but it turns out they are not very accurate. Do a search on “birthday paradox” and you’ll be surprised at what the actual answer is!

One final note about all the formulas in Stats: In most high school and undergraduate Stats classes, you learn the formulas without learning where they come from. That’s because the derivations often require difficult or tricky calculus or math analysis operations. But you can learn how to apply the formulas without knowing how to derive them, so most Stats classes are set up this way. If you are overwhelmed by all the formulas, keep a list handy that reminds you when each formula is used. This will help you tame your Statistics class.

Oct 06

Degrees vs. radians: which is “better”?

By Tutor GuyNo Comments

 

Both degrees and radians have their uses and you are probably more familiar with degrees, but only because you learned them first. By the time you get to calculus, you have to work in radians, so you need to be comfortable with them. And they’re not as confusing as they seem. Just as you can measure your height in inches or in centimeters, degrees and radians are just two different ways of measuring angles.

Trig will be easier if you learn to count in both degrees and radians. You probably already know that there are 360° in a circle. Now memorize that there are also 2π radians in a circle.

The only conversion you have to remember is that π radians = 180°. Then you can determine all the other special angles pretty quickly. For example, π/6 rad = 180°/6 = 30°. π/4 rad = 180°/4 = 45°. It’s that simple!

Oct 03

Finding reciprocals

By Tutor GuyNo Comments

 

Sep 29

Using l’Hôpital’s Rule

By Tutor GuyNo Comments

 

There are two guidelines you should always follow when applying l’Hôpital’s rule:

  • Make sure the original function gives you an indeterminate result before you take the derivatives;
  • Always simplify the result before plugging in to save yourself some extra work.

Example 1: Here’s a simple example that demonstrates the importance of the first guideline.

Find:

\displaystyle \lim_{x \to 0} \frac{x}{1+ \sin x}

 Solution: This function is continuous at x=0. To find the limit, simply plug in 0:

 \displaystyle \lim_{x \to 0} \frac{x}{1+ \sin x}=\frac{0}{1+0}=0

This is easily verified if you graph the function. However, if you try to apply l’Hôpital’s rule right away, you will get the incorrect value for the limit:

\displaystyle \lim_{x \to 0} \frac{x}{1+ \sin x}=\lim_{x \to 0} \frac{1}{\cos x}= \frac{1}{1}=1

 

Example 2: This example demonstrates the importance of the second guideline.

Find:

\displaystyle \lim_{x \to 0^+} \dfrac{\ln x}{^1 \!/ \!_x}

This satisfies the conditions for applying l’Hôpital’s rule, because plugging in gives an indeterminate form.

 

\displaystyle \lim_{x \to 0^+} \dfrac{\ln x}{^1 \!/ \!_x}=\frac{\ln 0}{^1 \! / _0}= \frac{-\infty}{\infty}

 We apply l’Hôpital’s rule once:

\displaystyle \lim_{x \to 0^+} \dfrac{\ln x}{^1 \!/ \!_x}= \lim_{x \to 0^+}\frac{1/x}{-1/x^2}

This would give us another indeterminate form if we plug in now, but we remember to simplify first, and it’s easy to evaluate:

 

\displaystyle \lim_{x \to 0^+} \dfrac{\ln x}{^1 \!/ \!_x}= \lim_{x \to 0^+}\frac{1/x}{-1/x^2}= \lim_{x \to 0^+} -x=0

Again, this is easy to verify by plotting the function.

Sep 26

Is it positive? increasing? concave up?

By Tutor GuyNo Comments

 

When you are asked to analyze a function in calculus, be sure to distinguish between positive/negative, increasing/decreasing, and concave up/concave down. These are three different concepts!

Here’s the same function, shown three times.

  • The value of the function determines whether it is positive or negative:

 

 

 

 

 

 

 

  • The value of the first derivative determines whether it is increasing or decreasing:

 

 

 

 

 

 

 

 

  • The value of the second derivative determines whether it is concave up or concave down:

Sep 22

Inverse of a 2×2 matrix

By Tutor GuyNo Comments

 

\left ( \begin{bmatrix} a & b \\ c & d \end{bmatrix} \right )^{-1} = \text{ ?}

 Instead of calculating the inverse of a 2 x 2 matrix, it’s easier to remember this simple manipulation:

  • Switch the a and d terms, and
  • change the signs on the b and c terms.
  • Then divide every term by the determinant (ad - bc). The result will be the inverse of the original matrix.

In general:

\left ( \begin{bmatrix} a & b \\ c & d \end{bmatrix} \right )^{-1} = \dfrac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}

 Example:

\left ( \begin{bmatrix} 2 & 1 \\ -3 & 7 \end{bmatrix} \right )^{-1} = \dfrac{1}{2 \cdot 7-1 \cdot (-3)} \begin{bmatrix} 7 & -1 \\ 3 & 2 \end{bmatrix} = \dfrac{1}{17} \begin{bmatrix} 7 & -1 \\ 3 & 2 \end{bmatrix}= \begin{bmatrix} ^7 \! / _{17} & ^{-1} \! / \! _{17} \\ ^3 \! / \! _{17} & ^2 \! / \! _{17} \end{bmatrix}

< OlderNewer >
Blue Taste Theme created by Jabox