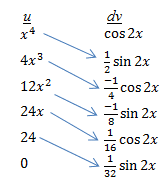Archive

Oct 09

Tabular integration

By Tutor GuyNo Comments

 

Occasionally, you will be faced with a complicated integral such as

\int x^4 \cos 2x \; dx

If you’ve read some of my other posts, you know that this requires integration by parts. Let’s get started on it and see where it leads.

\begin{matrix} u = x^4 & dv = \cos 2x \; dx \\ du = 4x^3 \; dx & v = \dfrac{\sin 2x}{2} \end{matrix}

Then (after a bit of simplifying),

\int x^4 \cos 2x \; dx = \dfrac{1}{2} x^4 \sin 2x - 2 \int x^3 \sin 2x \; dx

Now what? Well, the new integral requires integration by parts too! So you go through all the steps again. Then you have to do integration by parts on this result. And again on the next result! It’s tedious, but eventually you get to the correct answer. However, if one of the two functions in the original integral is a polynomial, there is a faster way to do this process. It’s called tabular integration, because all the parts of the integral are found by filling in a table.

Make a two-column table, with the columns labeled u and dv. Put the polynomial function (in our example, x4) under the u. Then take the derivative of this function and write it below the original function. Continue taking the derivative until you reach 0. In our example, your first column now looks like this.

\begin{matrix} \underline{u} & \underline{dv} \\ x^4 & \text{ } \\ 4x^3 & \text{ } \\ 12x^2 & \text{ } \\ 24x & \text { } \\ 24 & \text{ } \\ 0 & \text{ } \end{matrix}

Next, place the other function in the dv column. Integrate this function repeatedly until there are entries in every row. In our example, your completed table will look like this:

\begin{matrix} \underline{u} & \underline{dv} \\ x^4 & \cos 2x \\ \text{ } \\4x^3 & \frac{1}{2} \sin 2x \\ \text{ } \\12x^2 & \frac{-1}{4} \cos 2x \\ \text{ } \\24x & \frac{-1}{8} \sin 2x \\ \text{ } \\24 & \frac{1}{16} \cos 2x \\ \text{ } \\0 & \frac{1}{32} \sin 2x \end{matrix}

You’ve done all the hard work! Now you can write out the integral from the values in this table. First draw an arrow from each u value (except 0) to the dv value on the next line below, as shown here:

 

 

 

 

 

 

Next, place alternating plus and minus signs on each arrow:

 

 

 

 

 

 

Now multiply each u value by the dv value at the other end of the arrow. The plus or minus sign tells you whether to add or subtract this term. For this problem, the integral would be:

(x^4)(\frac{1}{2} \sin 2x) - (4x^3)(\frac{-1}{4} \cos 2x) + (12x^2)(\frac{-1}{8} \sin 2x) - (24x)(\frac{1}{16} \cos 2x) + (24)(\frac{1}{32} \sin 2x)

Simplifying gives the final answer (don’t forget the C!):

\frac{1}{2} x^4 \sin 2x \; + \; x^3 \cos 2x \; - \; \frac{3}{2} x^2 \sin 2x \; - \; \frac{3}{2} \cos 2x \; + \;  \frac{3}{4} \sin 2x \; + \; C 

 

Jan 12

How to approach integration by parts

By Tutor GuyNo Comments

 

In an earlier post, I described a strategy for approaching integrals and how to decide what technique to use. One question I suggested you ask yourself is “Can I use integration by parts?” In this post, I describe how you decide when integration by parts is the right approach, and how you decide which term will be u and which will be dv.

There is no product rule for integrals, but when you see an integrand that is the product of two functions [and u substitution has been ruled out], integration by parts is often the right approach. For example, each of the following integrals should be solved using integration by parts:

 \displaystyle \int x^2e^x \; dx \\ \displaystyle \int e^x \sin x \; dx \\ \displaystyle \int x \tan^{-1} x \; dx

Once you decide that integration by parts is the correct technique, does it matter which factor you make u and which you make dv? Usually, yes. But don’t worry if you make the wrong choice—you’ll know that pretty quickly. Remember that the purpose of integration by parts is to take a complicated integrand and make it simpler. If you choose your u and dv incorrectly, your integrand will get more complicated. When you find your integral getting worse, just start again and switch your choices for u and dv. (If switching choices doesn’t make your integral look better, perhaps integration by parts isn’t the proper technique for the integral.)

Here’s a trick to help you decide which factor should be the u term: LIPET. This is a mnemonic to help you determine the priority for assigning factors to be u. The acronym stands for the following:

L: logarithmic functions
I: inverse trigonometric functions
P: polynomials
E: exponential functions
T: trigonometric functions

For example, the first integral above is the product of a polynomial and an exponential function. P precedes E in LIPET, so make x2 the u term and ex the dv term. The third integral above is the product of a polynomial and an inverse trig function, so let tan-1 x be the u term and x will be the dv term.

Finally, note that even though integration by parts creates a simpler integral, it won’t always create an integral you can evaluate by inspection. Often, you will need to use another technique to integrate the new integrand, or perhaps you will need to do integration by parts a second time.

Blue Taste Theme created by Jabox