Archive

For the Precalc/Trig category

Sep 15

Trig functions: positive or negative?

By Tutor GuyNo Comments

 

Many students like to use the phrase “All Students Take Calculus” to help them remember where the various trig functions are positive or negative. Place the letters of these four words in quadrants I to IV as shown below.

  • The A in Quadrant I stands for “all functions” (sine, cosine & tangent) are positive in this quadrant.
  • The S in Quadrant II stands for “only sine” is positive in this quadrant.
  • The T in Quadrant III stands for “only tangent” is positive in this quadrant.
  • The C in Quadrant IV stands for “only cosine” is positive in this quadrant.

 

Another simple method is to remember that the cosine values are the x coordinates on the unit circle (and therefore positive in Quadrants I and IV) and the sine values are the y coordinates (and therefore positive in Quadrants I and II).

Sep 12

The Unit Circle

By Tutor GuyNo Comments

 

The sooner you memorize the sine, cosine and tangent of the special angles on the unit circle, the easier trig will be for you. Yes, you can always derive these values from the rules for special triangles you learned in geometry, but that is no substitute for memorizing the unit circle.

Sep 08

Taming trig identities

By Tutor GuyNo Comments

 

Proving trig identities is not as difficult as it looks if you follow these strategies.

1. The first thing you should look for is to factor one or both sides like a polynomial. This is not always possible, but simplifies the rest of the work.

2. If there are double angle functions [such as sin(2θ)] or sum of angle functions [such as sin(α + β)], expand these using the double angle or sum formulas.

3. Look for trig identities, and substitute them to simplify the expression.

4. If one side of the identity has two fractions added or subtracted, combine the fractions by finding a common denominator. (Then look for factors or identities as above.)

5. When in doubt, convert everything to sines and cosines. Then try to simplify the resulting expression.

6. If the expression contains 1 + sin θ or 1 + cos θ, consider multiplying top and bottom by the “conjugate”: 1 – sin θ or 1 – cos θ. This will give you a trig identity you can simplify.

7. When you get one side as simple as it can get, start on the other side.

8. Don’t give up! If you aren’t making the expression simpler, cross it out and try another strategy.

 

Example: Here’s a (rather complicated) example. Don’t panic! Watch how we can use all of the strategies above to solve the identity step by step.

Prove the identity:

\dfrac{2 \tan \theta + 2 \sin \theta \tan \theta}{\sec \theta \sin 2 \theta}= \dfrac{\cos^3 \theta}{2-2 \sin \theta} \left ( \dfrac{1}{1- \sin \theta}+ \dfrac{1}{1+ \sin \theta} \right )

 Think you can do it? Sure you can! The first thing you do is factor. Start with the left side, and you see you can factor 2 tan θ out of the numerator:

\dfrac{2 \tan \theta (1+ \sin \theta)}{\sec \theta \sin 2 \theta}= \dfrac{\cos^3 \theta}{2-2 \sin \theta} \left ( \dfrac{1}{1- \sin \theta}+ \dfrac{1}{1+ \sin \theta} \right )

 Strategy 2 says to expand double angle formulas.  Change the sin 2θ in the denominator:

\dfrac{2 \tan \theta (1+ \sin \theta)}{\sec \theta (2 \sin \theta \cos \theta)}= \dfrac{\cos^3 \theta}{2-2 \sin \theta} \left ( \dfrac{1}{1- \sin \theta}+ \dfrac{1}{1+ \sin \theta} \right )

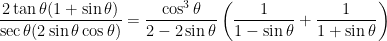
 There are no identities on the left side (strategy 3), so go to strategy 4 and convert the tan θ and sec θ into sines and cosines:

\dfrac{2 \sin \theta \cos \theta (1+ \sin \theta)}{\cos \theta (2 \sin \theta \cos \theta)}= \dfrac{\cos^3 \theta}{2-2 \sin \theta} \left ( \dfrac{1}{1- \sin \theta}+ \dfrac{1}{1+ \sin \theta} \right )

 Now let’s simplify the left side before moving on:

\dfrac{1+ \sin \theta}{\cos \theta}= \dfrac{\cos^3 \theta}{2-2 \sin \theta} \left ( \dfrac{1}{1- \sin \theta}+ \dfrac{1}{1+ \sin \theta} \right )

 That’s about as simple as you can make the left side.  Strategy 7 says to move to the other side. The first thing to do is factor a 2 out of the 2 – 2 sin θ term in the denominator:

\dfrac{1+ \sin \theta}{\cos \theta}= \dfrac{\cos^3 \theta}{2(1-\sin \theta)} \left ( \dfrac{1}{1- \sin \theta}+ \dfrac{1}{1+ \sin \theta} \right )

 Next, strategy 4 says to combine the sum of the two fractions by finding a common denominator:

\dfrac{1+ \sin \theta}{\cos \theta}= \dfrac{\cos^3 \theta}{2(1-\sin \theta)} \left ( \dfrac{1+ \sin \theta}{(1- \sin \theta)(1+ \sin \theta)}+ \dfrac{1- \sin \theta}{(1- \sin \theta)(1+ \sin \theta)} \right )

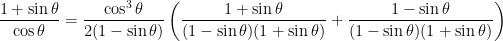
 Let’s simplify that mess in the parentheses (notice that we multiply out the two factors in the denominator):

\dfrac{1+ \sin \theta}{\cos \theta}= \dfrac{\cos^3 \theta}{2(1-\sin \theta)} \left ( \dfrac{2}{1- \sin^2 \theta} \right )

 Now we have an identity (strategy 3)! Substitute cos2 θ for 1-sin2 θ in the denominator and cancel with the cos3 θ. Cancel the 2 on the top and bottom also:

\dfrac{1+ \sin \theta}{\cos \theta}= \dfrac{\cos \theta}{1-\sin \theta}

 We’ve simplified both sides significantly, but they’re not the same yet. Here’s where we apply strategy 6 by multiplying top and bottom of the left side by 1 – sin θ and simplifying:

\dfrac{1- \sin \theta}{1- \sin \theta} \cdot \dfrac{1+ \sin \theta}{\cos \theta}= \dfrac{\cos \theta}{1-\sin \theta}

\dfrac{1- \sin^2 \theta}{(1- \sin \theta) \cos \theta} = \dfrac{\cos \theta}{1-\sin \theta}

\dfrac{\cos^2 \theta}{(1- \sin \theta) \cos \theta} = \dfrac{\cos \theta}{1-\sin \theta}

\dfrac{\cos \theta}{1- \sin \theta} = \dfrac{\cos \theta}{1-\sin \theta}

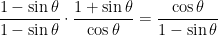
 Hey, we did it! We have tamed a very difficult identity by methodically applying the strategies at the top of this page one after another!

Aug 30

Finding angles in radians

By Tutor GuyNo Comments

 

Finding the location of an angle on the unit circle in radians is a lot easier if you imagine counting in multiples of π/2, π/3, π/4 or π/6. For example, to figure out where 5π/3 is on the unit circle, count out “one π/3, two π/3, three π/3 (which is π), four π/3, five π/3.” You’ll get to the right spot every time!

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Of course, to make this process work, you do need to know the following relationships

  • π/2 = 90°
  • π/3 = 60°
  • π/4 = 45°
  • π/6 = 30°
Newer >
Blue Taste Theme created by Jabox