The most valuable first step when doing a related rate problem is to draw a picture. This helps you figure out the geometry of the problem.
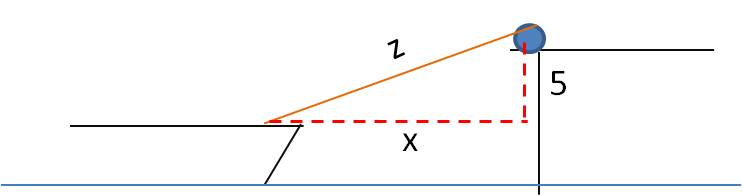
Example: A boat is being towed to a dock by a rope attached to a winch that is five feet higher than the boat. If the winch is pulling the rope at 1.2 m/s, how fast is the boat moving when it is 12 m from the dock?
Solution: It would be very difficult to set up and solve this problem without a quick sketch. But once you draw the picture (and label the components as shown), you can see that a simple right triangle describes the situation.
The equation you need is therefore:
Differentiating gives:
So the boat is approaching the dock at 1.3 m/s.
(Look for other tips on solving related rate problems if you need help with some of the details of the solution.)